Техника - молодёжи 2009-08, страница 10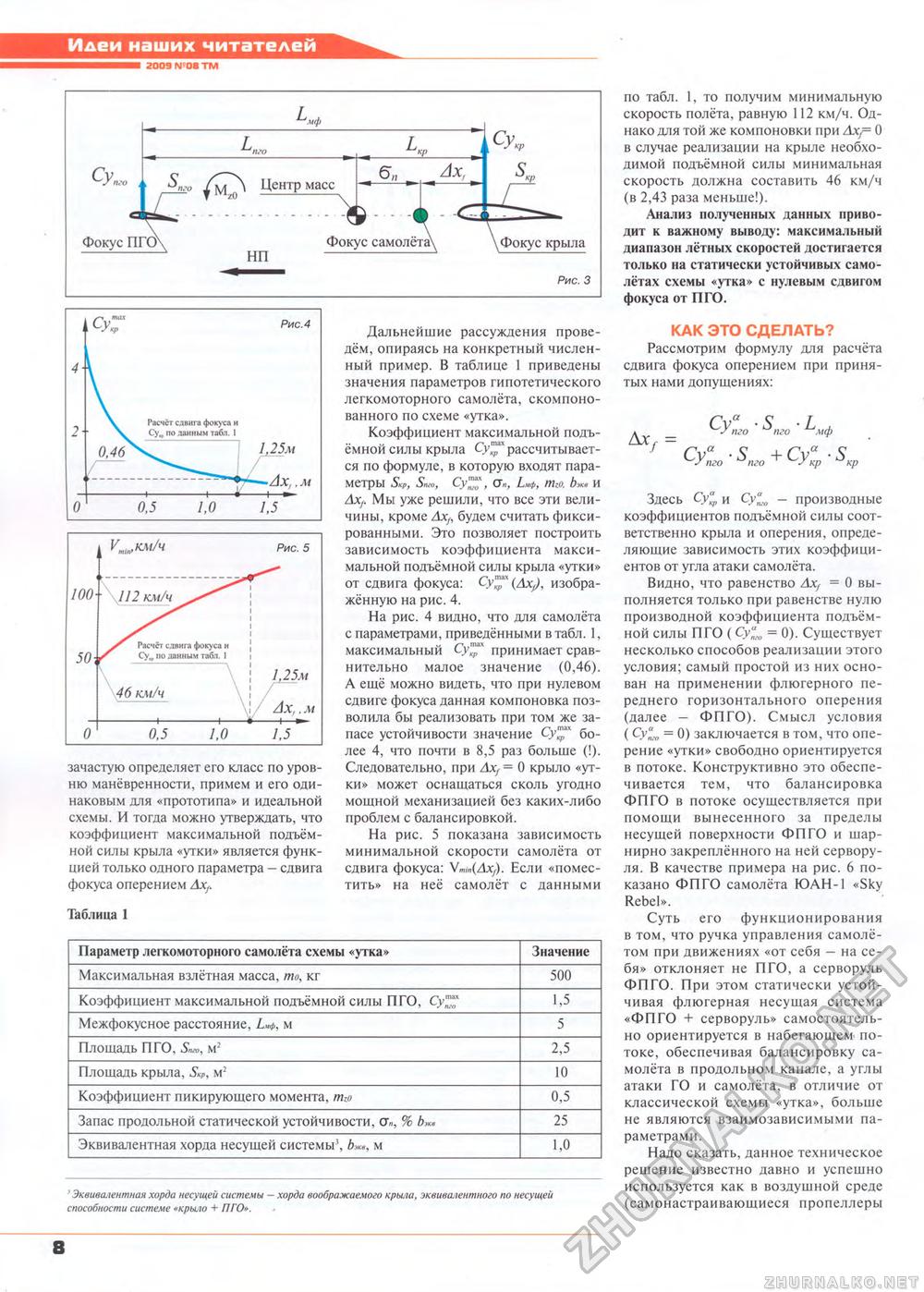
Идеи наших читателей 2009 №0И ТМ
зачастую определяет его класс по уровню манёвренности, примем и его одинаковым для «прототипа» и идеальной схемы. И тогда можно утверждать, что коэффициент максимальной подъёмной силы крыла «утки» является функцией только одного параметра - сдвига фокуса оперением Axf. Таблица 1 Дальнейшие рассуждения проведём, опираясь на конкретный численный пример. В таблице 1 приведены значения параметров гипотетического легкомоторного самолёта, скомпонованного по схеме «утка». Коэффициент максимальной подъёмной силы крыла Су™ рассчитывается по формуле, в которую входят параметры Sup, Snm, Су, о1,,, Ьнф, mzo. Ьж* и АхР Мы уже решили, что все эти величины, кроме Axf, будем считать фиксированными. Это позволяет построить зависимость коэффициента максимальной подъёмной силы крыла «утки» от сдвига фокуса: Су™1 (Axf), изображённую на рис. 4. На рис. 4 видно, что для самолёта с параметрами, приведёнными в табл. J, максимальный Су™" принимает сравнительно малое значение (0,46), А ещё можно видеть, что при нулевом сдвиге фокуса данная компоновка позволила бы реализовать при том же запасе устойчивости значение С/™ более 4, что почти в 8,5 раз больше (!). Следовательно, при Ах/ = 0 крыло «утки» может оснащаться сколь угодно мощной механизацией без каких-либо проблем с балансировкой. На рис. 5 показана зависимость минимальной скорости самолёта от сдвига фокуса: V^Axj). Если «поместить» на неё самолёт с данными по табл. 1, то получим минимальную скорость полёта, равную 112 км/ч. Однако для той же компоновки при Axj= 0 в случае реализации на крыле необходимой подъёмной силы минимальная скорость должна составить 46 км/ч {в 2,43 раза меньше!). Анализ полученных данных приводит к важному выводу: максимальный диапазон лётных скоростей достигается только на статически устойчивых самолётах схемы «утка» с нулевым сдвигом фокуса от Г1ГО. КАК ЭТО СДЕЛАТЬ? Рассмотрим формулу для расчёта сдвига фокуса оперением при принятых нами допущениях: Суа • S L , __у то то мф Здесь Су*р и Су^ — производные коэффициентов подъёмной силы соответственно крыла и оперения, определяющие зависимость этих коэффициентов от угла атаки самолёта. Видно, что равенство Ах( = 0 выполняется только при равенстве нулю производной коэффициента подъёмной силы ПГО (Су= 0). Существует несколько способов реализации этого условия; самый простой из них основан на применении флюгерного переднего горизонтального оперения (далее — ФПГО). Смысл условия ( = 0) заключается в том, что оперение «утки» свободно ориентируется в потоке. Конструктивно это обеспечивается тем, что балансировка ФПГО в потоке осуществляется при помоши вынесенного за пределы несущей поверхности ФПГО и шар-нирно закреплённого на ней сервору-ля, В качестве примера на рис. 6 показано ФПГО самолёта ЮАН-1 «Sky Rebel». Суть его функционирования в том, что ручка управления самолётом при движениях «от себя — на себя» отклоняет не ПГО. а серворуль ФПГО. При этом статически устойчивая флюгерная несущая система «ФПГО + серворуль» самостоятельно ориентируется в набегающем- потоке, обеспечивая балансировку самолёта в продольном канале, а углы атаки ГО и самолёта, в отличие от классической схемы «утка», больше не являются взаимозависимыми параметрами. Надо сказать, данное техническое решение известно давно и успешно используется как в воздушной среде (самонастраивающиеся пропеллеры Таблица 1
: Эквивалентная хорда несущей системы — хорда воображаемого крыла, эквивалентного по несущей способности системе *крыяо + ПГО*. : Эквивалентная хорда несущей системы — хорда воображаемого крыла, эквивалентного по несущей способности системе *крыяо + ПГО*. 8 |








