Советы профессионалов 2004-06, страница 47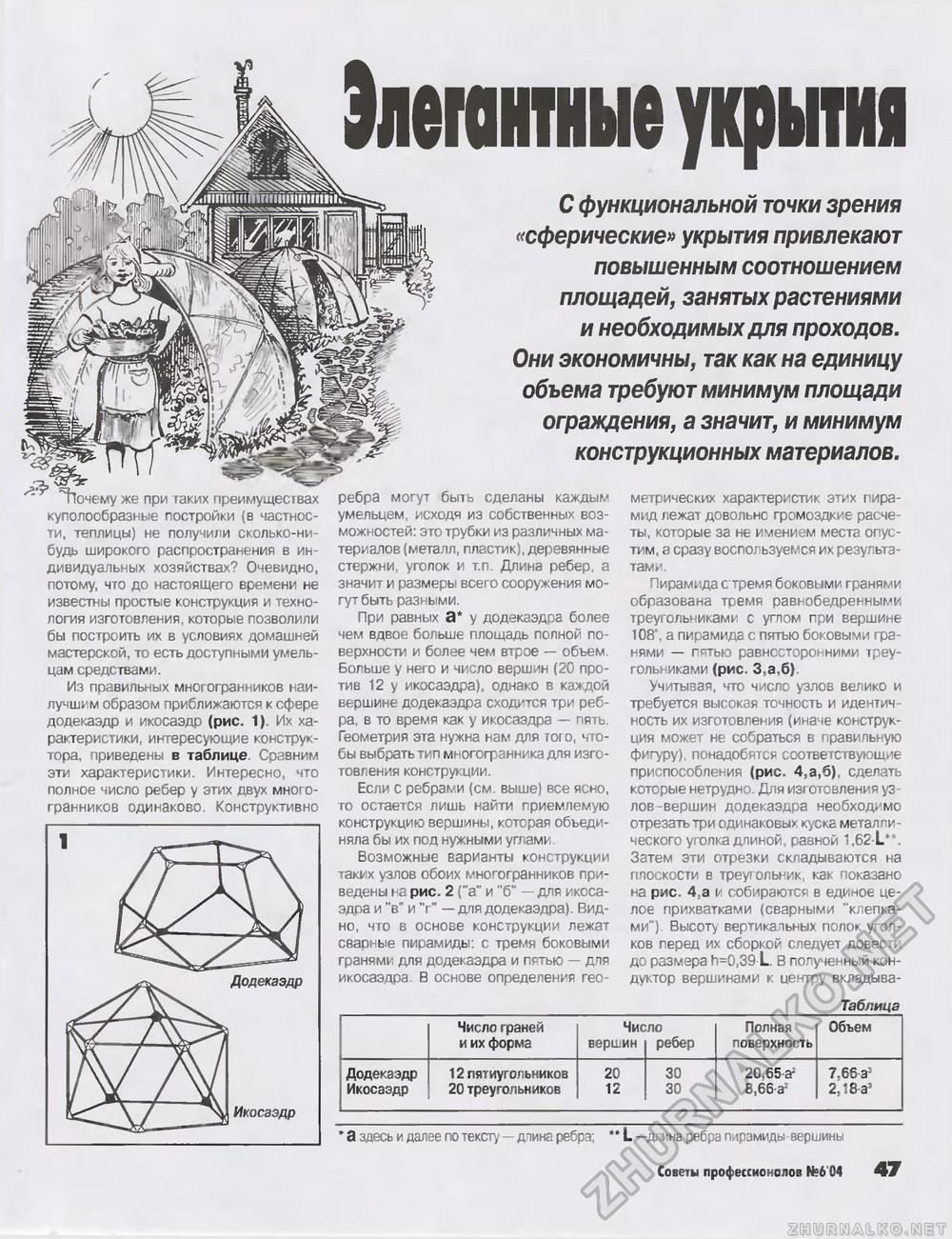
Элегантные укрытия С функциональной точки зрения «сферические»укрытия привлекают повышенным соотношением площадей, занятых растениями и необходимых для проходов. Они экономичны, так как на единицу объема требуют минимум площади ограждения, а значит, и минимум конструкционных материалов. Почему же при таких преимуществах куполообразные постройки (в частности, теплицы) не получили сколько-нибудь широкого распространения в индивидуальных хозяйствах? Очевидно, потому, что до настоящего времени не известны простые конструкция и технология изготовления которые позволили бы построить их в условиях домашней мастерской, то есть доступными умельцам средствами. Из правильных многогранников наилучшим образом приближаются к сфере додекаэдр и икосаэдр (рис. 1) Их характеристики, интересующие конструктора, приведены в таблице. Сравним эти характеристики. Интересно, что полное число ребер у этих двух многогранников одинаково Конструктивно ребра могут быть сделаны каждым умельцем исходя из собственных возможностей: это трубки из различных материалов (металл, пластик), деревянные стержни, уголок и т.п. Длина ребер, а значит и размеры всего сооружения могут быть разными. При равных а* у додекаэдра более чем вдвое больше площадь полной поверхности и более чем втрое — объем. Больше у него и число вершин (20 против 12 у икосаэдра), однако в каждой вершине додекаэдра сходится три ребра, в то время как у икосаэдра — пять. Геометрия эта нужна нам для toi о, чтобы выбрать тип многогранника для изготовления конструкции. Если с ребрами (см. выше) все ясно, то остается лишь найти приемлемую конструкцию вершины, которая объединяла бы их под нужными углами Возможные варианты конструкции таких узлов обоих многогранников приведены на рис. 2 ("а" и "б" — для икоса-эдпа и "в" и "г" — для додекаэдра). Видно, что в основе конструкции лежат сварные пирамиды: с тремя боковыми гранями для додекаэдра и пятью — для икосаэдра. В основе определения гео метрических характеристик этих пирамид j.ежат довольнс громоздкие расчеты, которые за не имением места опустим, а сразу воспользуемся их результатами. Пирамида с тремя боковыми гранями образована тремя равнобедренными треугольниками с углом при вершине 108°. а пирамида с пятью боковыми гранями — пятью равносторонними треугольниками (рис. 3,а,б). Учитывая, что число узлов велико и требуется высокая точность и идечтич ■ ность их изготовления (иначе конструкция может не собраться в правильную фигуру), понадобятся соответствующие приспособления (рис. 4,а,6), сделать которые нетрудно. Для изготовления узлов -вершин додекаэдра необходимо отрезать три одинаковых куска металчи-ческого уголка длиной, равной 1,62 L". Затем эти отрезки складываются на плоскости в треуюльник, как показано на рис 4,а и собираются в единое целое прихватками (сварными "ю.епка-ми"] Высоту вертикальных полок уголков перед их сборкой следует довести до размера h=0,39-L. В полученный кондуктор вершинами к центру вкладыва Табпица Табпица
* 3 здесь и далее по тексту — дпина ребра; " L —длина ребра пирамиды вершины Советы профессионалов №6'04 47 |
||||||||||||||||||||||||








