Техника - молодёжи 1987-05, страница 54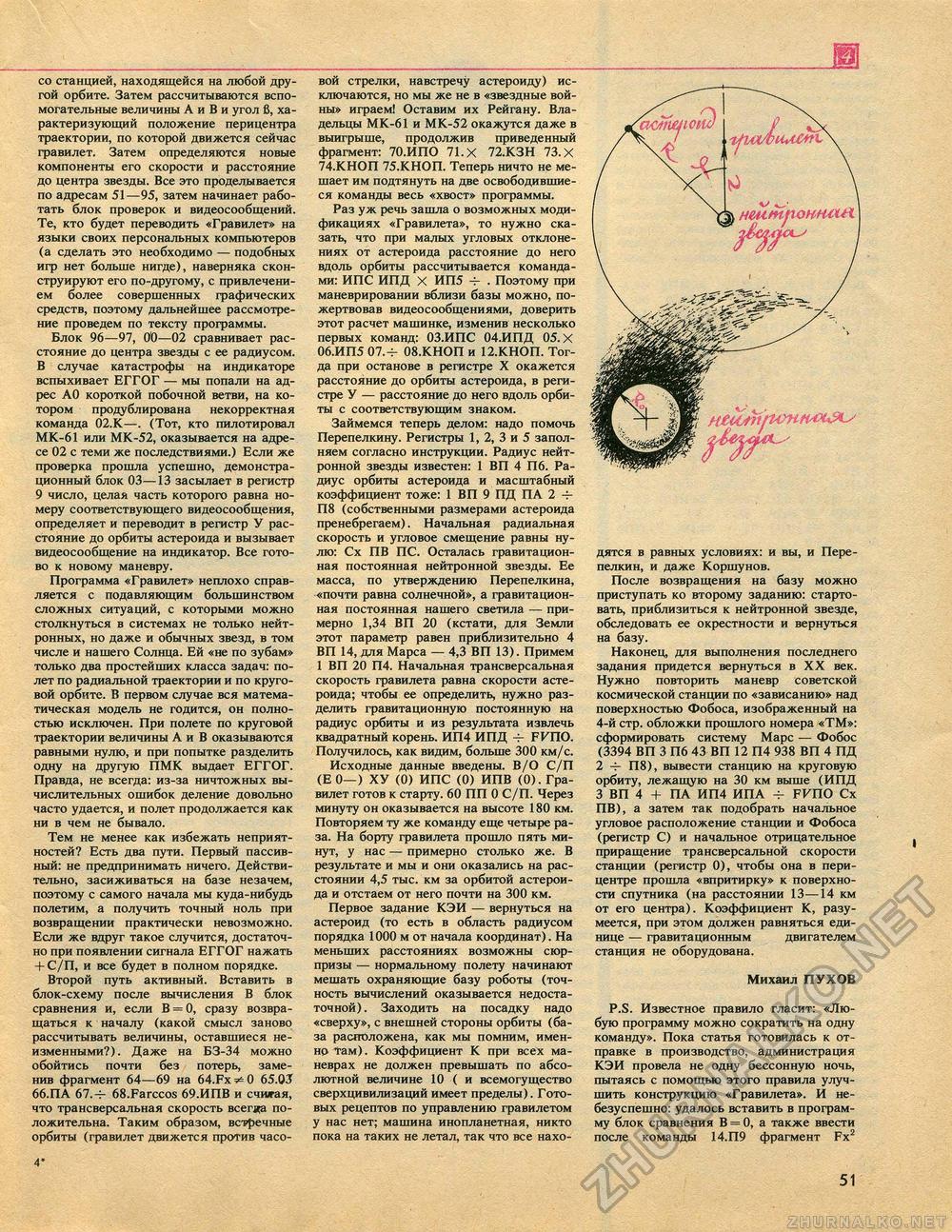

со станцией, находящейся на любой другой орбите. Затем рассчитываются вспомогательные величины А и В и угол 6, характеризующий положение перицентра траектории, по которой движется сейчас гравилет. Затем определяются новые компоненты его скорости и расстояние до центра звезды. Все это проделывается по адресам 51—95, затем начинает работать блок проверок и видеосообщений. Те, кто будет переводить «Гравилет» на языки своих персональных компьютеров (а сделать это необходимо — подобных игр нет больше нигде), наверняка сконструируют его по-другому, с привлечением более совершенных графических средств, поэтому дальнейшее рассмотрение проведем по тексту программы.

Блок 96—97, №—02 сравнивает расстояние до центра звезды с ее радиусом. В случае катастрофы на индикаторе вспыхивает ЕГГОГ — мы попали на адрес АО короткой побочной ветви, на котором продублирована некорректная команда 02.К—. (Тот, кто пилотировал МК-61 или МК-52, оказывается на адресе 02 с теми же последствиями.) Если же проверка прошла успешно, демонстрационный блок 03—13 засылает в регистр 9 число, целая часть которого равна номеру соответствующего видеосообщения, определяет и переводит в регистр У расстояние до орбиты астероида и вызывает видеосообщение на индикатор. Все готово к новому маневру.

Программа «Гравилет» неплохо справляется с подавляющим большинством сложных ситуаций, с которыми можно столкнуться в системах не только нейтронных, но даже и обычных звезд, в том числе и нашего Солнца. Ей «не по зубам» только два простейших класса задач: полет по радиальной траектории и по круговой орбите. В первом случае вся математическая модель не годится, он полностью исключен. При полете по круговой траектории величины А и В оказываются равными нулю, и при попытке разделить одну на другую ПМК выдает ЕГГОГ. Правда, не всегда: из-за ничтожных вычислительных ошибок деление довольно часто удается, и полет продолжается как ни в чем не бывало.

Тем не менее как избежать неприятностей? Есть два пути. Первый пассивный: не предпринимать ничего. Действительно, засиживаться на базе незачем, поэтому с самого начала мы куда-нибудь полетим, а получить точный ноль при возвращении практически невозможно. Если же вдруг такое случится, достаточно при появлении сигнала ЕГГОГ нажать + С/П, и все будет в полном порядке.

Второй путь активный. Вставить в блок-схему после вычисления В блок сравнения и, если В = 0, сразу возвращаться к началу (какой смысл заново рассчитывать величины, оставшиеся неизменными?). Даже на Б3-34 можно обойтись почти без потерь, заменив фрагмент 64—69 на 64.Fx Ф 0 65.03 66.ПА 67.-Ь 68.Farccos 69.ИПВ и считая, что трансверсальная скорость всегда положительна. Таким образом, встречные орбиты (гравилет движется против часо

4*

вой стрелки, навстречу астероиду) исключаются, но мы же не в «звездные войны» играем! Оставим их Рейгану. Владельцы МК-61 и МК-52 окажутся даже в выигрыше, продолжив приведенный фрагмент: 70.ИПО 71. X 72.КЗН 73. X 74.КНОП 75.КНОП. Теперь ничто не мешает им подтянуть на две освободившиеся команды весь «хвост» программы.

Раз уж речь зашла о возможных модификациях «Гравилета», то нужно сказать, что при малых угловых отклонениях от астероида расстояние до него вдоль орбиты рассчитывается командами: ИПС ИПД X ИП5 . Поэтому при маневрировании вблизи базы можно, пожертвовав видеосообщениями, доверить этот расчет машинке, изменив несколько первых команд: ОЗ.ИПС 04.ИПД 05. X 06.ИП5 07.-Ь 08.КНОП и 12.КНОП. Тогда при останове в регистре X окажется расстояние до орбиты астероида, в регистре У — расстояние до него вдоль орбиты с соответствующим знаком.

Займемся теперь делом: надо помочь Перепелкину. Регистры 1, 2, 3 и 5 заполняем согласно инструкции. Радиус нейтронной звезды известен: 1 ВП 4 П6. Радиус орбиты астероида и масштабный коэффициент тоже: 1 ВП 9 ПД ПА 2 4-П8 (собственными размерами астероида пренебрегаем). Начальная радиальная скорость и угловое смещение равны нулю: Сх ПВ ПС. Осталась гравитационная постоянная нейтронной звезды. Ее масса, по утверждению Перепелкина, «почти равна солнечной», а гравитационная постоянная нашего светила — примерно 1,34 ВП 20 (кстати, для Земли этот параметр равен приблизительно 4 ВП 14, для Марса — 4,3 ВП 13). Примем 1 ВП 20 П4. Начальная трансверсальная скорость гравилета равна скорости астероида; чтобы ее определить, нужно разделить гравитационную постоянную на радиус орбиты и из результата извлечь квадратный корень. ИП4 ИПД FFnO. Получилось, как видим, больше 300 км/с.

Исходные данные введены. В/О С/П (Е0—) ХУ (0) ИПС (0) ИПВ (0). Гравилет готов к старту. 60 ПП 0 С/П. Через минуту он оказывается на высоте 180 км. Повторяем ту же команду еще четыре раза. На борту гравилета прошло пять минут, у нас — примерно столько же. В результате и мы и они оказались на расстоянии 4,5 тыс. км за орбитой астероида и отстаем от него почти на 300 км.

Первое задание КЭИ — вернуться на астероид (то есть в область радиусом порядка 1000 м от начала координат). На меньших расстояниях возможны сюрпризы — нормальному полету начинают мешать охраняющие базу роботы (точность вычислений оказывается недостаточной). Заходить на посадку надо «сверху», с внешней стороны орбиты (база расположена, как мы помним, именно там). Коэффициент К при всех маневрах не должен превышать по абсолютной величине 10 (и всемогущество сверхцивилизаций имеет пределы). Готовых рецептов по управлению гравилетом у нас нет; машина инопланетная, никто пока на таких не летал, так что все нахо

дятся в равных условиях: и вы, и Пере-пелкин, и даже Коршунов.

После возвращения на базу можно приступать ко второму заданию: стартовать, приблизиться к нейтронной звезде, обследовать ее окрестности и вернуться на базу.

Наконец, для выполнения последнего задания придется вернуться в XX век. Нужно повторить маневр советской космической станции по «зависанию» над поверхностью Фобоса, изображенный на 4-й стр. обложки прошлого номера «ТМ»: сформировать систему Марс — Фобос (3394 ВП 3 П6 43 ВП 12 П4 938 ВП 4 ПД

2 — П8), вывести станцию на круговую орбиту, лежащую на 30 км выше (ИПД

3 ВП 4 + ПА ИП4 ИПА -4- FJ-TIO Сх ПВ), а затем так подобрать начальное угловое расположение станции и Фобоса (регистр С) и начальное отрицательное приращение трансверсальной скорости станции (регистр 0), чтобы она в перицентре прошла «впритирку» к поверхности спутника (на расстоянии 13—14 км от его центра). Коэффициент К, разумеется, при этом должен равняться единице — гравитационным двигателем станция не оборудована.

Михаил ПУХОВ

P.S. Известное правило гласит: «Любую программу можно сократить на одну команду». Пока статья готовилась к отправке в производство, администрация КЭИ провела не одну бессонную ночь, пытаясь с помощью этого правила улучшить конструкцию «Гравилета». И небезуспешно: удалось вставить в программу блок сравнения В = 0, а также ввести после команды 14.П9 фрагмент Fx²

51