Техника - молодёжи 1957-06, страница 21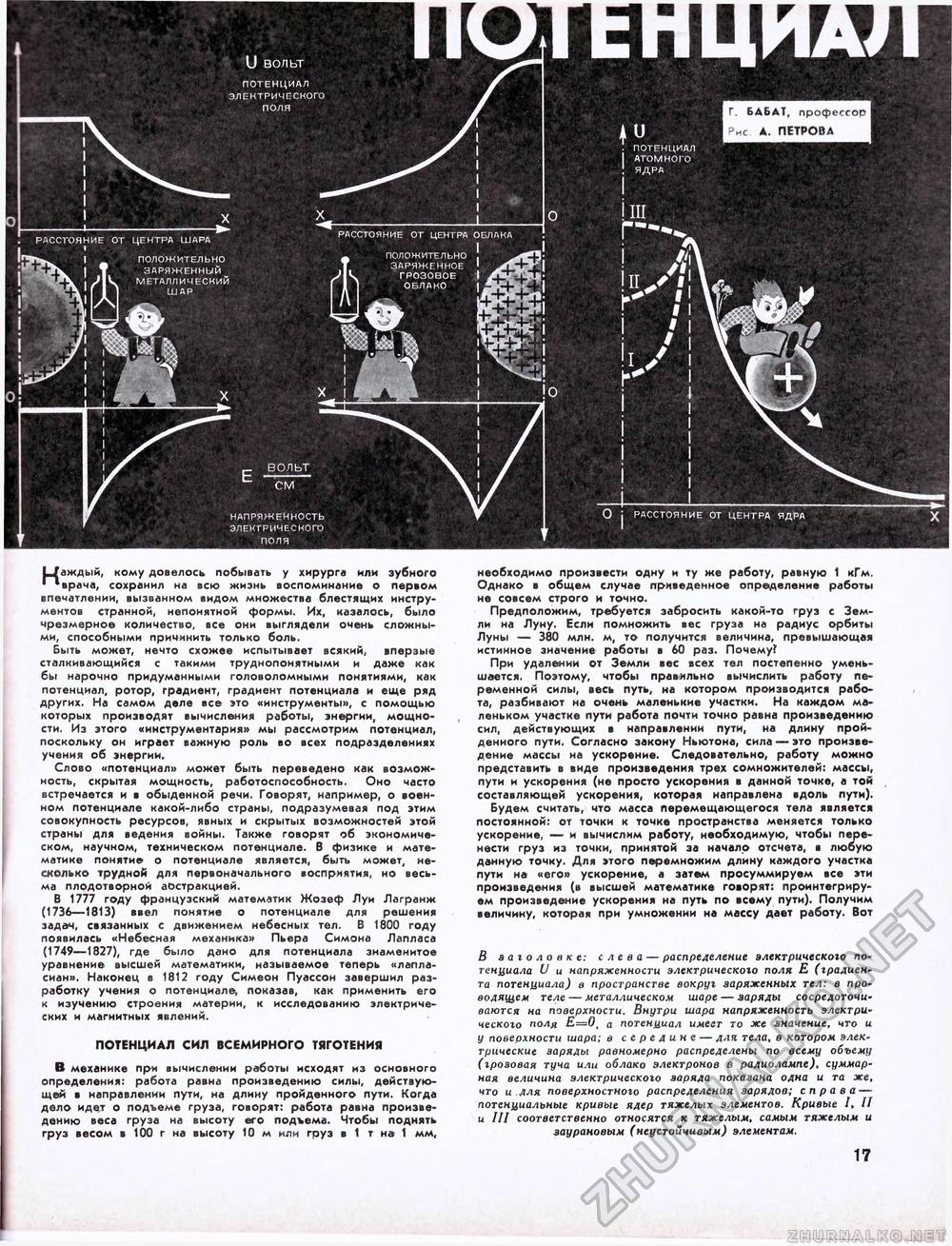
U вольт ПОТЕНЦИАЛ ЭЛЕКТРИЧЕСКОГО ПОЛЯ ПОТЕНЦИАЛ АТОМНОГО Г. Б дБ AT, профессор Рис А. ПЕТРОВА РАССТОЯНИЕ ОТ ЦЕНТРА ШАРА Ifc. | ПОЛОЖИТЕЛЬНО J Т ЗАРЯЖЕННЫЙ fcPV I /МЧ МЕТАЛЛИЧЕСКИЙ П 1 шар РАССТОЯНИЕ ОТ ЦЕНТРА ПОЛОЖИТЕЛЬНО ЗАРЯЖЕННОЕ ГРОЗОВОЕ ОБЛАКО ОБЛАКА I ВОЛЬТ НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО РАССТОЯНИЕ ОТ ЦЕНТРА ЯДРА L/аждый, кому довелось побывать у хирурга или зубного ■ • врача, сохранил на всю жизнь воспоминание о первом впечатлении, вызванном видом множества блестящих инструментов странной, непонятной формы. Их, казалось, было чрезмерное количество, все они выглядели очень сложными, способными причинить только боль. Быть может, нечто схожее испытывает всякий, впервые сталкивающийся с такими труднопонятными и даже как бы нарочно придуманными головоломными понятиями, как потенциал, ротор, градиент, градиент потенциала и еще ряд других. На самом деле все это «инструменты», с помощью которых производят вычисления работы, энергии, мощности. Из этого «инструментария» мы рассмотрим потенциал, поскольку он играет важную роль во всех подразделениях учения об энергии. Слово «потенциал» может быть переведено как возможность, скрытая мощность, работоспособность. Оно часто встречается и в обыденной речи. Говорят, например, о военном потенциале какой-либо страны, подразумевая под этим совокупность ресурсов, явных и скрытых возможностей этой страны для ведения войны. Также говорят об экономическом, научном, техническом потенциале. В физике и математике понятие о потенциале является, быть может, несколько трудной для первоначального восприятия, но весьма плодотворной абстракцией. В 1777 году французский математик Жозеф Луи Лагранж (1736—1813) ввел понятие о потенциале для решения задач, связанных с движением небесных тел. В 1800 году появилась «Небесная механика» Пьера Симона Лапласа (1749—1827), где было дано для потенциала знаменитое уравнение высшей математики, называемое теперь «лапласиан». Наконец в 1812 году Симеон Пуассон завершил разработку учения о потенциале, показав, как применить его к изучению строения материи, к исследованию электрических и магнитных явлений. ПОТЕНЦИАЛ СИЛ ВСЕМИРНОГО ТЯГОТЕНИЯ В механике при вычислении работы исходят из основного определения: работа равна произведению силы, действующей в направлении пути, на длину пройденного пути. Когда дело идет о подъеме груза, говорят: работа равна произведению веса груза на высоту его подъема. Чтобы поднять груз весом в 100 г на высоту 10 м или груз в 1 т на 1 мм, необходимо произвести одну и ту же работу, равную 1 кГм. Однако в общем случае приведенное определение работы не совсем строго и точно. Предположим, требуется забросить какой-то груз с Земли на Луну. Если помножить вес груза на радиус орбиты Луны — 380 млн. м, то получится величина, превышающая истинное значение работы в 60 раз. Почему? При удалении от Земли вес всех тел постепенно уменьшается. Поэтому, чтобы правильно вычислить работу переменной силы, весь путь, на котором производится работа, разбивают на очень маленькие участки. На каждом маленьком участке пути работа почти точно равна произведению сил, действующих в направлении пути, на длину пройденного пути. Согласно закону Ньютона, сила — это произведение массы на ускорение. Следовательно, работу можно представить в виде произведения трех сомножителей: массыг пути и ускорения (не просто ускорения в данной точке, а той составляющей ускорения, которая направлена вдоль пути). Будем считать, что масса перемещающегося тела является постоянной: от точки к точке пространства меняется только ускорение, — и вычислим работу, необходимую, чтобы перенести груз из точки, принятой за начало отсчета, в любую данную точку. Для этого перемножим длину каждого участка пути на «его» ускорение, а затем просуммируем все эти произведения (в высшей математике говорят: проинтегрируем произведение ускорения на путь по всему пути). Получим величину, которая при умножении на массу дает работу. Вот В заголовке: слева — распределение электрического потенциала U и напряженности электрического поля Е (градиента потенциала) в пространстве вокруг заряженных тел: в проводящем теле — металлическом шаре — заряды сосредоточиваются на поверхности. Внутри шара напряженность электрического поля E~0f а потенциал имеет то же значение, что и у поверхности шара; в середине — для тела, в котором электрические заряды равномерно распределены по всему объему (грозовая туча или облако электронов в радиолампе), суммарная величина электрического заряда показана одна и та же, что и для поверхностного распределения зарядов; справа — потенциальные кривые ядер тяжелых элементов. Кривые /» // и III соответственно относятся к тяжелым, самым тяжелым и заурановым (неустойчивым) элементам. 17 |








