Техника - молодёжи 1971-10, страница 67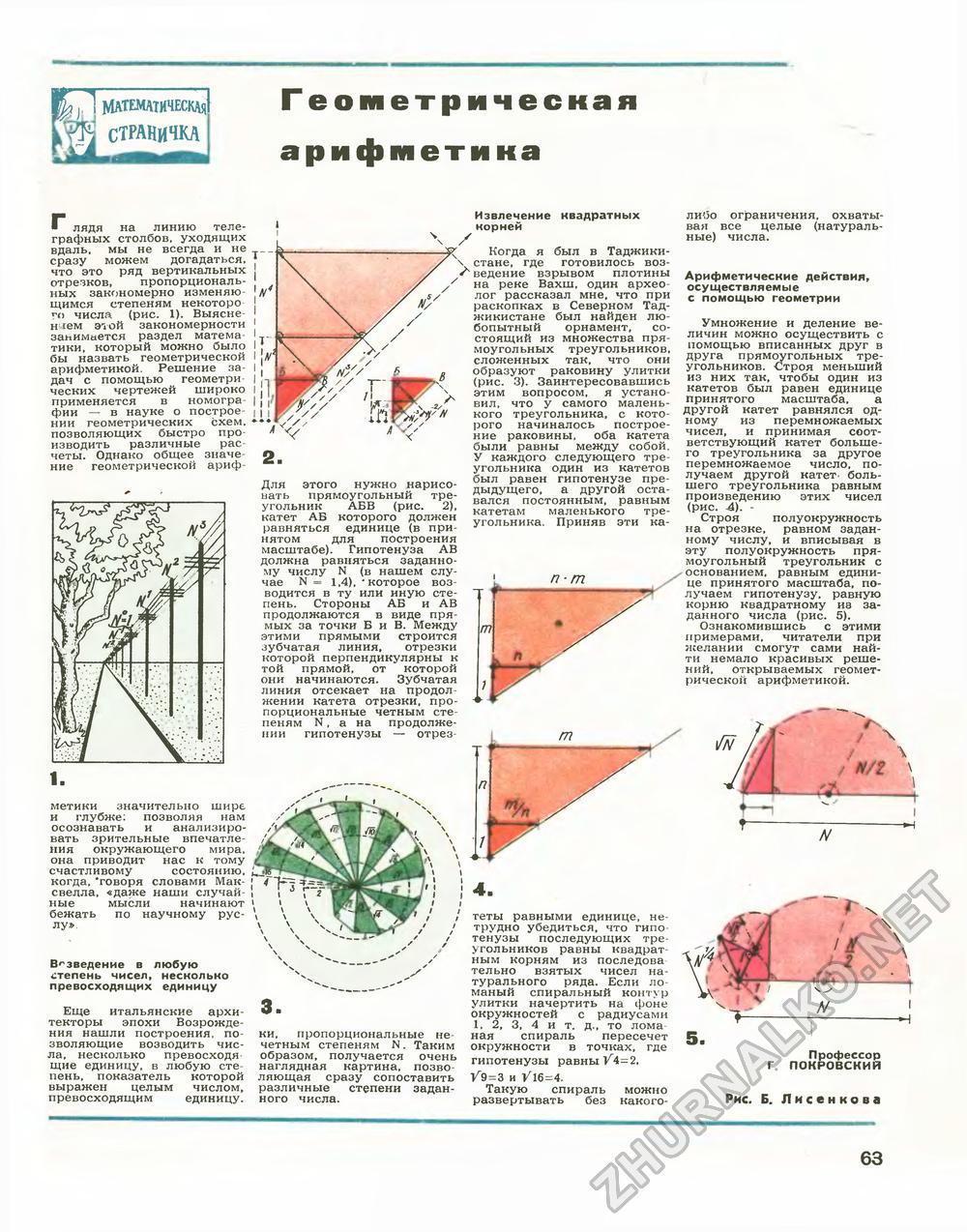
Геометрическая арифметика ■ лядя на линию телеграфных столбов, уходящих вдаль, мы не всегда и не сразу можем догадаться, что это ряд вертикальных отрезков, пропорциональных закономерно изменяющимся степеням некоторо го числя (рис. 1). Выяснением этой закономерности занимается раздел математики, который можно было бы назвать геометрической арифметикой. Решение задач с помощью геометри ческих чертежей широко применяется в номографии — в науке о построении геометрических схем. позволяющих быстро производить различные расчеты. Однако общее значение геометрической ариф- Для этого нужно нарисовать прямоугольный треугольник^ АБВ (рис. 2) Извлечение квадратных корней Когда я был в Таджики-\ стане, где готовилось воз-ведение взрывом плотины на реке Вахш, один археолог рассказал мне, что при раскопках в Северном Таджикистане был найден любопытный орнамент, состоящий из множества прямоугольных треугольников, сложенных так, что они образуют раковину улитки (рис. 3). Заинтересовавшись этим вопросом, я установил, что у самого маленького треугольника, с которого начиналось построение раковины, оба катета были равны между собой. У каждого следующего треугольника один из катетов был равен гипотенузе предыдущего, а другой оставался постоянным, равным катетам маленького тре- катет АБ которого должен Угольника Птэиняв эти ка равняться единице (в при- Угольника. Приняв эти ка нятом для построения масштабе). Гипотенуза АВ должна равняться заданному числу N (в нашем случае N = 1,4), 'которое возводится в ту или иную степень. Стороны АБ и АВ продолжаются в виде прямых за точки Б и В. Между этими прямыми строится зубчатая линия, отрезки которой перпендикулярны к той прямой, от которой они начинаются. Зубчатая линия отсекает на продолжении катета отрезки, пропорциональные четным степеням N, а на продолжении гипотенузы — отрез- метики значительно шире и глубже: позволяя нам осознавать и анализировать зрительные впечатления окружающего мира, она приводит нас к тому счастливому состоянию, __ когда, 'говоря словами Мак- j 4 свелла, «даже наши случай- \ • г •» ные мысли начинают \ бежать »w/»_ лу». по научному рус- В^зведение в любую степень чисел, несколько превосходящих единицу Еще итальянские архитекторы эпохи Возрождения нашли построения, позволяющие возводить числа, несколько превосходя щие единицу, в любую степень, показатель которой выражен целым числом, превосходящим единицу. У 3. ки, пропорциональные нечетным степеням N. Таким образом, получается очень наглядная картина, позволяющая сразу сопоставить различные степени заданного числа. п - т либо ограничения, охватывая все целые (натуральные) числа. Арифметические действия, осуществляемые с помощью геометрии Умножение и деление величин можно осуществить с помощью вписанных друг в друга прямоугольных треугольников. Строя меньший из них так, чтобы один из катетов был равен единице принятого масштаба, а другой катет равнялся одному из перемножаемых чисел, и принимая соответствующий катет большего треугольника за другое перемножаемое число, получаем другой катет- большего треугольника равным произведению этих чисел (рис. 4). - Строя полуокружность на отрезке, равном заданному числу, и вписывая в эту полуокружность прямоугольный треугольник с основанием, равным единице принятого масштаба, получаем гипотенузу, равную корню квадратному ив заданного числа (рис. 5). Ознакомившись с этими примерами, читатели при желании смогут сами найти немало красивых решений, открываемых геометрической арифметикой. 4. теты равными единице, нетрудно убедиться, что гипотенузы последующих треугольников равны квадратным корням из последова тельно взятых чисел натурального ряда. Если ломаный спиральный контур улитки начертить на фоне окружностей с радиусами 1, 2, 3, 4 и т. д., то лома ная спираль пересечет окружности в точках, где гипотенузы равны 1/9=3 и 1/16=4. Такую спираль можно развертывать без какого- /Ч \ N/Z \ -tfL 1 N \ // \ ' 1 . \ N Профессор ЖРОВСКИ ~ Г ПОКРОВСКИЙ Рис. Б. Яисенкова 63 |








