Техника - молодёжи 1969-08, страница 21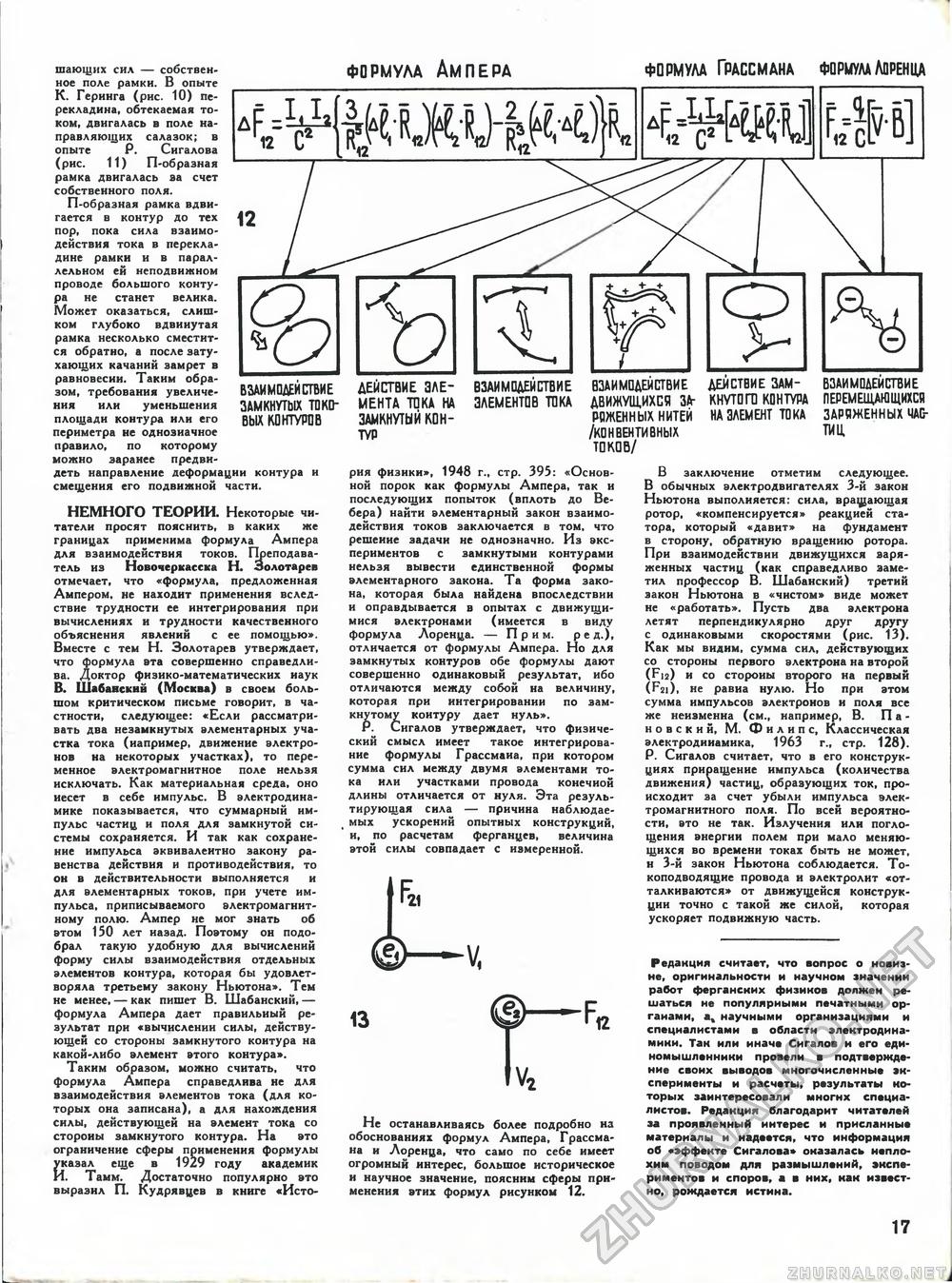
ВЗАИМОДЕИСТВИЕ ЗАМКНУТЫХ токовых КОНТУРОВ шающих сил — собственное поле рамки. В опыте К. Геринга (рис. 10) перекладина, обтекаемая током, двигалась в поле направляющих салазок; в опыте Р. Сигалова (рис. 11) П-образная рамка двигалась за счет собственного поля. П-образная рамка вдвигается в контур до тех пор, пока сила взаимодействия тока в перекладине рамки и в параллельном ей неподвижном проводе большого контура не станет велика. Может оказаться, слишком глубоко вдвинутая рамка несколько сместится обратно, а после затухающих качаний замрет в равновесии. Таким образом, требования увеличения или уменьшения площади контура или его периметра не однозначное правило, по которому можно заранее предвидеть направление деформации контура и смещения его подвижной части. НЕМНОГО ТЕОРИИ. Некоторые читатели просят пояснить, в каких же границах применима формула Ампера для взаимодействия токов. Преподаватель из Новочеркасска Н. Золотарев отмечает, что «формула, предложенная Ампером, не находит применения вследствие трудности ее интегрирования при вычислениях и трудности качественного объяснения явлений с ее помощью». Вместе с тем Н. Золотарев утверждает, что формула эта совершенно справедлива. Доктор физико-математических наук В. Шабаискни (Москва) в своем большом критическом письме говорит, в частности, следующее: «Если рассматривать два незамкнутых элементарных участка тока (например, движение электронов на некоторых участках), то переменное электромагнитное поле нельзя исключать. Как материальная среда, оно несет в себе импульс. В электродинамике показывается, что суммарный импульс частиц и поля для замкнутой системы сохраняется. И так как сохранение импульса эквивалентно закону равенства действия и противодействия, то он в действительности выполняется и для элементарных токов, при учете импульса, приписываемого электромагнитному полю. Ампер не мог знать об этом 150 лет назад. Поэтому он подобрал такую удобную для вычислений форму силы взаимодействия отдельных элементов контура, которая бы удовлетворяла третьему закону Ньютона». Тем не менее, — как пишет В. Шабанский, — формула Ампера дает правильный результат при «вычислении силы, действующей со стороны замкнутого контура на какой-либо элемент этого контура». Таким образом, можно считать, что формула Ампера справедлива не для взаимодействия элементов тока (для которых она записана), а для нахождения силы, действующей на элемент тока со стороны замкнутого контура. На это ограничение сферы применения формулы указал еще в 1929 году академик И. Тамм. Достаточно популярно это выразил П. Кудрявцев в книге «Исто- формула Ампера формула Грассмана формула Лоренца ДЕЙСТВИЕ ЭЛЕМЕНТА ТОКА НА ЗАМКНУТЫЙ КОНТУР ВЗАИМОДЕИСТВИЕ ЭЛЕМЕНТОВ ТОКА ВЗАИМОДЕЙСТВИЕ ДЕЙСТВИЕ ЗАМ- ВЗАИМОДЕЙСТВИЕ ДВИЖУЩИХСЯ ЗА- КНУТОГО КОНТУРА ПЕРЕМЕЩАЮЩИХСЯ РЯЖЕННЫХ НИТЕЙ НА ЭЛЕМЕНТ ТОКА ЗАРЯЖЕННЫХ ЧАС-/КОНВЕНТИВНЫХ ТИЦ ТОКОВ/ рия физики», 1948 г., стр. 395: «Основной порок как формулы Ампера, так и последующих попыток (вплоть до Ве-бера) найти элементарный закон взаимодействия токов заключается в том, что решение задачи не однозначно. Из экспериментов с замкнутыми контурами нельзя вывести единственной формы элементарного закона. Та форма закона, которая была найдена впоследствии и оправдывается в опытах с движущимися электронами (имеется в виду формула Лоренца. — Прим. ре д.), отличается от формулы Ампера. Но для замкнутых контуров обе формулы дают совершенно одинаковый результат, ибо отличаются между собой на величину, которая при интегрировании по замкнутому контуру дает нуль». Р. Сигалов утверждает, что физический смысл имеет такое интегрирование формулы Грассмаиа, при котором сумма сил между двумя элементами тока или участками провода конечной длины отличается от нуля. Эта результирующая сила — причина наблюдае-( мых ускорений опытных конструкций, и, по расчетам ферганцев, величина этой силы совпадает с измеренной. IF* ©-V, В заключение отметим следующее. В обычных электродвигателях 3-й закон Ньютона выполняется: сила, вращающая ротор, «компенсируется» реакцией статора, который «давит» на фундамент в сторону, обратную вращению ротора. При взаимодействии движущихся заряженных частиц (как справедливо заметил профессор В. Шабанский) третий закон Ньютона в «чистом» виде может не «работать». Пусть два электрона летят перпендикулярно друг другу с одинаковыми скоростями (рис. 13). Как мы видим, сумма сил, действующих со стороны первого электрона на второй (F12) и со стороны второго на первый (F2i), не равна нулю. Но при этом сумма импульсов электронов и поля все же неизменна (см., например, В. Панов с к и й, М. Филипс, Классическая электродинамика, 1963 г., стр. 128). Р. Сигалов считает, что в его конструкциях приращение импульса (количества движения) частиц, образующих ток, происходит за счет убыли импульса электромагнитного поля. По всей вероятности, это не так. Излучения или поглощения энергии полем при мало меняющихся во времени токах быть не может, и 3-й закон Ньютона соблюдается. То-коподводящие провода и электролит «отталкиваются» от движущейся конструкции точно с такой же силой, которая ускоряет подвижную часть. 13 Не останавливаясь более подробно на обоснованиях формул Ампера, Грассмана н Лоренца, что само по себе имеет огромный интерес, большое историческое и научное значение, поясним сферы применения этих формул рисунком 12. Редакция считает, что вопрос о новизне, оригинальности и научном значении работ ферганских физиков должен решаться не популярными печатными органами, а% научными организациями и специалистами в области электродинамики. Так или инача Сигалов и его единомышленники провели в подтверждение своих выводов многочисленные эксперименты и расчеты, результаты которых заинтересовали многих специалистов. Редакция благодарит читателей за проявленный интерес и присланные материалы и надеется, что информация об «эффекте Сигалова» оказалась неплохим поводом для размышлений, экспериментов и споров, а в них, как известно, рождается истина. 17 |








