Техника - молодёжи 1982-07, страница 23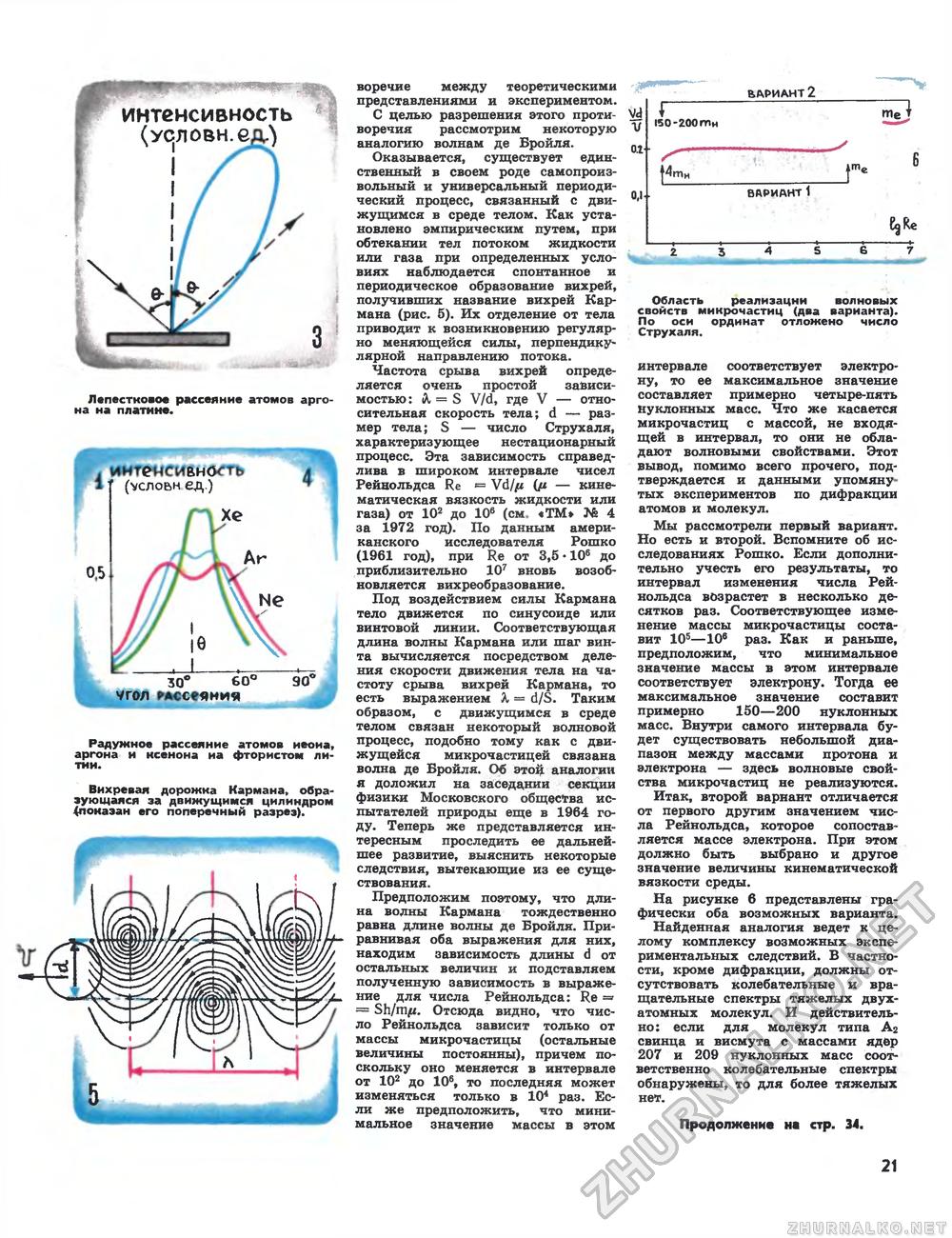

интенсивность

(условн.ед.)

В*»--

Лепестковое рассеяние атомов аргона на платине.

30" 60^е УГОЛ РАССЕЯНИЯ

90

Радужное рассеяние атомов иеоиа, аргона и ксенона на фтористом литии.

Вихревая дорожка Кармана, образующаяся за движущимся цилиндром {показан его поперечный разрез).

воречие между теоретическими представлениями и экспериментом.

С целью разрешения этого противоречия рассмотрим некоторую аналогию волнам де Бройля.

Оказывается, существует единственный в своем роде самопроизвольный и универсальный периодический процесс, связанный с движущимся в среде телом. Как установлено эмпирическим путем, при обтекании тел потоком жидкости или газа при определенных условиях наблюдается спонтанное и периодическое образование вихрей, получивших название вихрей Кармана (рис. 5). Их отделение от тела приводит к возникновению регулярно меняющейся силы, перпендикулярной направлению потока.

Частота срыва вихрей определяется очень простой зависимостью: А, = S V/d, где V — относительная скорость тела; d — размер тела; S — число Струхаля, характеризующее нестационарный процесс. Эта зависимость справедлива в широком интервале чисел Рейнольдса Re Vd/fi {jjl — кинематическая вязкость жидкости или газа) от 10² до 10⁶ (см. «ТМ» № 4 за 1972 год). По данным американского исследователя Рошко (1961 год), при Re от 3,5 • 10⁶ до приблизительно 10⁷ вновь возобновляется вихреобразование.

Под воздействием силы Кармана тело движется по синусоиде или винтовой линии. Соответствующая длина волны Кармана или шаг винта вычисляется посредством деления скорости движения тела на частоту срыва вихрей Кармана, то есть выражением Я — d/S. Таким образом, с движущимся в среде телом связан некоторый волновой процесс, подобно тому как с движущейся микрочастицей связана волна де Бройля. Об этой аналогии я доложил на заседании секции физики Московского общества испытателей природы еще в 1964 году. Теперь же представляется интересным проследить ее дальнейшее развитие, выяснить некоторые следствия, вытекающие из ее существования.

Предположим поэтому, что длина волны Кармана тождественно равна длине волны де Бройля. Приравнивая оба выражения для них, находим зависимость длины d от остальных величин и подставляем полученную зависимость в выражение для числа Рейнольдса: Re = Sh/mji. Отсюда видно, что число Рейнольдса зависит только от массы микрочастицы (остальные величины постоянны), причем поскольку оно меняется в интервале от 10² до 10⁶, то последняя может изменяться только в 10⁴ раз. Если же предположить, что минимальное значение массы в этом

0,1

вариант 2

150 -200 т_и

те:

tl

т_н

вариант 1

eg Re

2 3 4 S 6 7

Область реализации волновых свойств микрочастиц (два варианта). По оси ординат отложено число Струхаля.

интервале соответствует электрону, то ее максимальное значение составляет примерно четыре-пять нуклонных масс. Что же касается микрочастиц с массой, не входящей в интервал, то они не обладают волновыми свойствами. Этот вывод, помимо всего прочего, подтверждается и данными упомянутых экспериментов по дифракции атомов и молекул.

Мы рассмотрели первый вариант. Но есть и второй. Вспомните об исследованиях Рошко. Если дополнительно учесть его результаты, то интервал изменения числа Рейнольдса возрастет в несколько десятков раз. Соответствующее изменение массы микрочастицы составит 10⁵—10⁶ раз. Как и раньше, предположим, что минимальное значение массы в этом интервале соответствует электрону. Тогда ее максимальное значение составит примерно 150—200 нуклонных масс. Внутри самого интервала будет существовать небольшой диапазон между массами протона и электрона — здесь волновые свойства микрочастиц не реализуются.

Итак, второй вариант отличается от первого другим значением числа Рейнольдса, которое сопоставляется массе электрона. При этом должно быть выбрано и другое значение величины кинематической вязкости среды.

На рисунке 6 представлены графически оба возможных варианта.

Найденная аналогия ведет к целому комплексу возможных экспериментальных следствий. В частности, кроме дифракции, должны отсутствовать колебательные и вращательные спектры тяжелых двухатомных молекул. И действительно: если для молекул типа Аг свинца и висмута с массами ядер 207 и 209 нуклонных масс соответственно колебательные спектры обнаружены, то для более тяжелых нет.

Продолжение не стр. 34.

21