Техника - молодёжи 1983-01, страница 25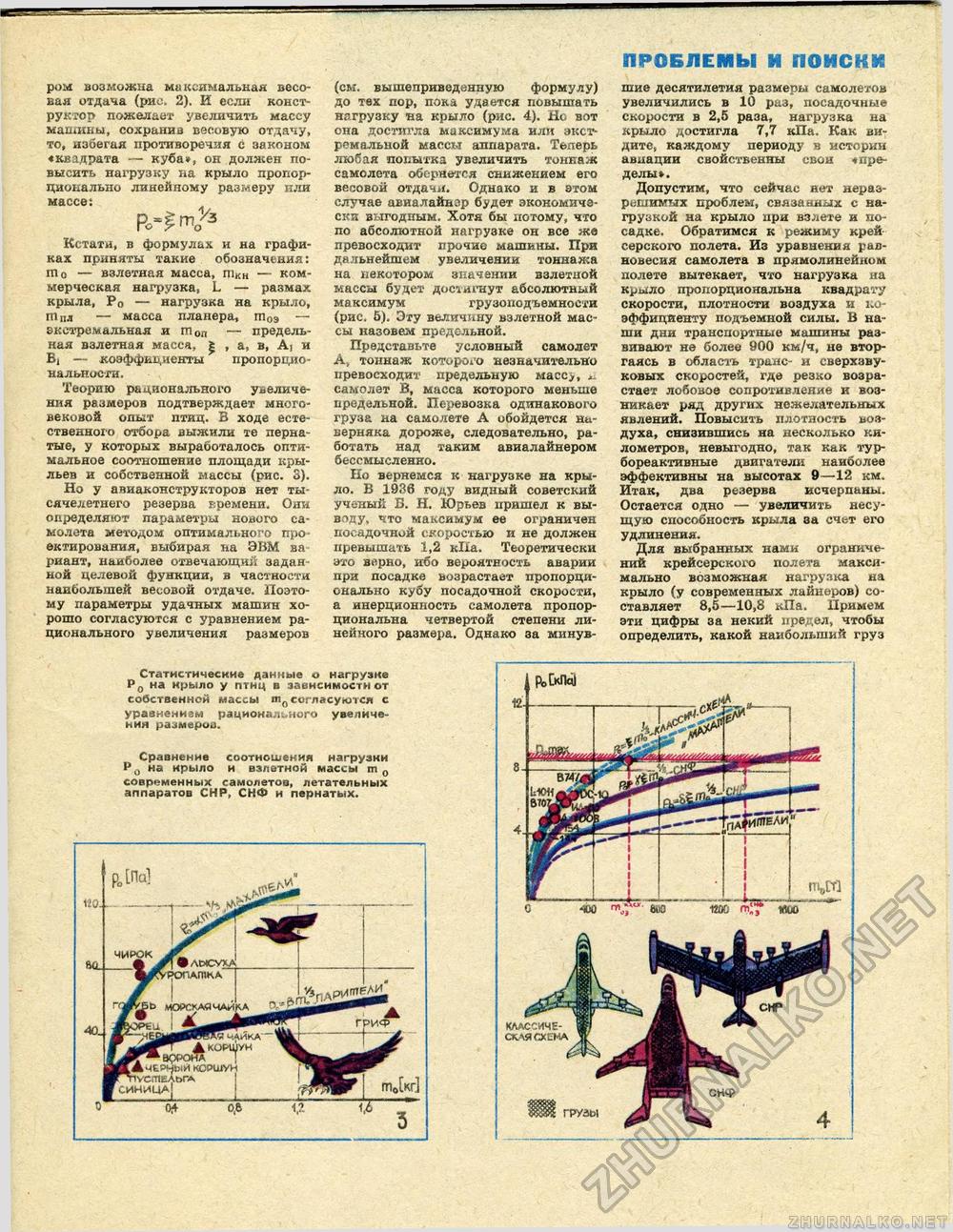

ПРОБЛЕМЫ И ПОИСКИ

ром возможна максимальная весовая отдача (рис. 2). И если конструктор пожелает увеличить массу машины, сохранив весовую отдачу, то, избегая противоречия с законом «квадрата — куба», он должен повысить нагрузку па крыло пропорционально линейному размеру или массе:

Р^т/з

Кстати, в формулах и на графиках приняты такие обозначения: in о — взлетная масса, m_KH — коммерческая нагрузка, L — размах крыла, Р₀ — нагрузка на крыло, Шпл — масса планера, ш₀э — экстремальная и ш₀п — предельная взлетная масса, £ , а, в, А, и В, — коэффициенты пропорциональности.

Теорию рационального увеличения размеров подтверждает многовековой опыт птиц. В ходе естественного отбора выжили те пернатые, у которых выработалось оптимальное соотношение площади крыльев и собственной массы (рис. S).

Но у авиаконструкторов нет тысячелетнего резерва времени. Они определяют параметры нового самолета методом оптимального проектирования, выбирая на ЭВМ ва риант, наиболее отвечающий заданной целевой функции, в частности наибольшей весовой отдаче. Поэтому параметры удачных машин хорошо согласуются с уравнением рационального увеличения размеров

(см. вышеприведенную формулу) до тех пор, пока удается повышать нагрузку на крыло (рис. 4). Но вот она достигла максимума или экстремальной массы аппарата. Теперь любая попытка увеличить тоннаж самолета обернется снижением его весовой отдачи. Однако и в этом случае авиалайнер будет экономически выгодным. Хотя бы потому, что по абсолютной нагрузке он все же превосходит прочие машины. При дальнейшем увеличении тоннажа на некотором значении взлетной массы будет достигнут абсолютный максимум грузоподъемности

(рис. б). Эту величину взлетной массы назовем предельной.

Представьте условный самолет А. тоннаж которого незначительно превосходит предельную массу, д. самолет В, масса которого меньше предельной. Перевозка одинакового груза на самолете А обойдется наверняка дороже, следовательно, работать над таким авиалайнером бессмысленно.

Но вернемся к нагрузке на крыло. В 1938 году видный советский ученый В. Н. Юрьев пришел к выводу, что максимум ее ограничен посадочной скоростью и не должен превышать 1,2 кПа. Теоретически это верно, ибо вероятность аварии при посадке возрастает пропорционально кубу посадочной скорости, а инерционность самолета пропорциональна четвертой степени линейного размера. Однако за минув

шие десятилетия размеры самолетов увеличились в 10 раз, посадочные скорости в 2,5 раза, нагрузка на крыло достигла 7,7 кПа. Как видите, каждому периоду в истории авиации свойственны свои «пределы».

Допустим, что сейчас нет неразрешимых проблем, связанных с нагрузкой на крыло при взлете и посадке, Обратимся к режиму крейсерского полета. Из уравнения равновесия самолета в прямолинейном полете вытекает, что нагрузка на крыло пропорциональна квадрату скорости, плотности воздуха и коэффициенту подъемной силы. В наши дни транспортные машины развивают не более 900 км/ч, не вторгаясь в область транс- и сверхзвуковых скоростей, где резко возрастает лобовое сопротивление и возникает ряд других нежелательных явлений. Повысить плотность воз-духа, снизившись на несколько километров, невыгодно, так как турбореактивные двигатели наиболее эффективны на высотах 9—12 км. Итак, два резерва исчерпаны. Остается одно — увеличить несущую способность крыла ва счет его удлинения.

Для выбранных нами ограничений крейсерского полета максимально возможная нагрузка на крыло (у современных лайнеров) составляет 8,5—10,8 кПа. Примем эти цифры за некий предел, чтобы определить, какой наибольший груз

Статистические данные о нагрузке Р₀ на крыло у птиц в зависимости от собственной массы ш₀ согласуются с уравнением рационального увеличения размере*).

Сравнение соотношения нагрузки Р₀ на крыло и взлетной массы ш₀ современных самолетов, летательных аппаратов СНР, СНФ и пернатых.