Техника - молодёжи 1989-02, страница 21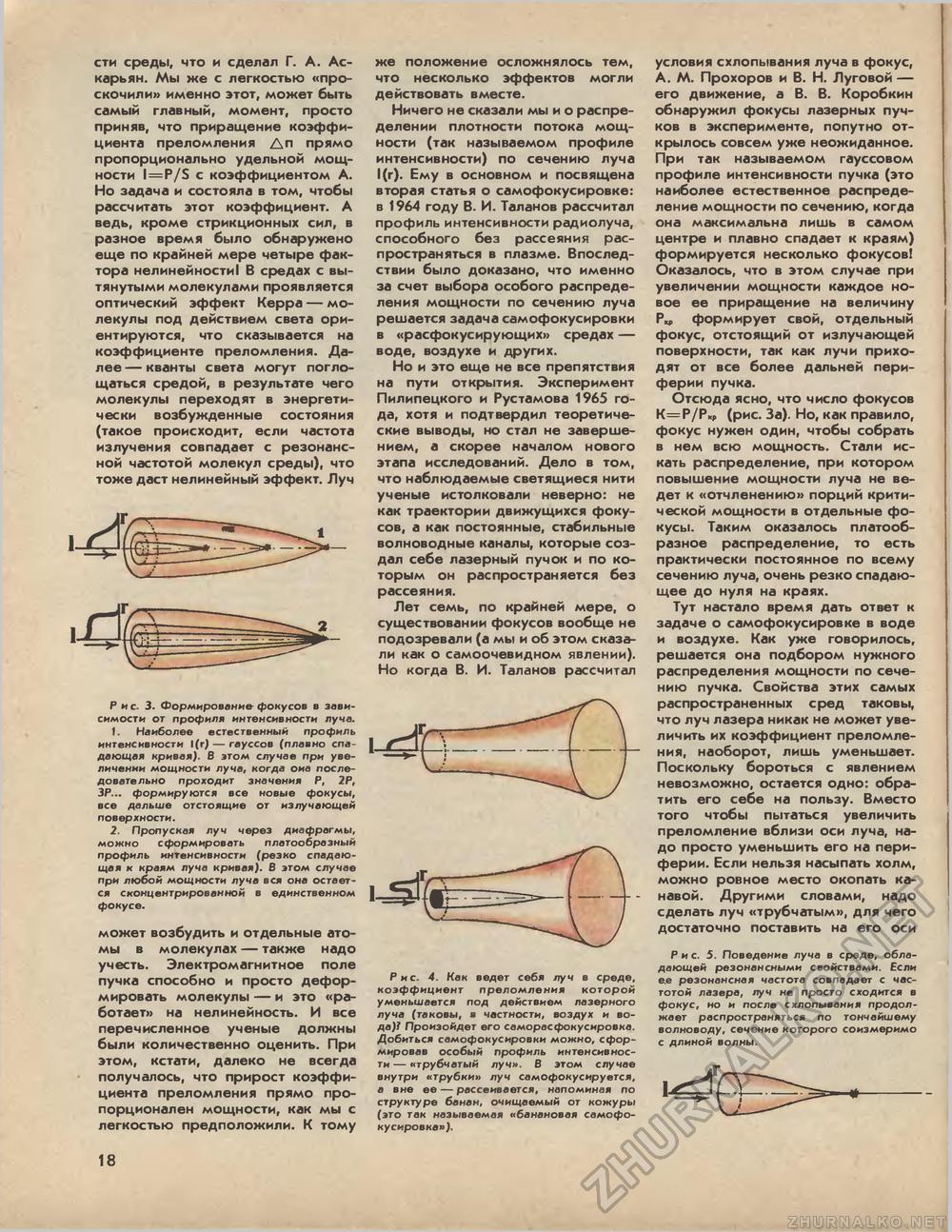

сти среды, что и сделал Г. А. Ас-карьян. Мы же с легкостью «проскочили» именно этот, может быть самый главный, момент, просто приняв, что приращение коэффициента преломления Дп прямо пропорционально удельной мощности l = P/S с коэффициентом А. Но задача и состояла в том, чтобы рассчитать этот коэффициент. А ведь, кроме стрикционных сил, в разное время было обнаружено еще по крайней мере четыре фактора нелинейности! В средах с вытянутыми молекулами проявляется оптический эффект Керра — молекулы под действием света ориентируются, что сказывается на коэффициенте преломления. Далее — кванты света могут поглощаться средой, в результате чего молекулы переходят в энергетически возбужденные состояния (такое происходит, если частота излучения совпадает с резонансной частотой молекул среды), что тоже даст нелинейный эффект. Луч

Рис. 3. Формирование фокусов в зависимости от профиля интенсивности пуча.

1. Наиболее естественный профиль интенсивности 1(г) — гауссов (плавно спадающая кривая). В этом случае при увеличении мощности луча, когда она последовательно проходит значения Р, 2Р, ЗР... формируются все новые фокусы, все дальше отстоящие от излучающей поверхности.

2. Пропуская луч через диафрагмы, можно сформировать платообразный профиль интенсивности (резко спадающая к краям луча кривая). В этом случае при любой мощности луча вся она остается сконцентрированной в единственном фокусе.

может возбудить и отдельные атомы в молекулах — также надо учесть. Электромагнитное поле пучка способно и просто деформировать молекулы — и это «работает» на нелинейность. И все перечисленное ученые должны были количественно оценить. При этом, кстати, далеко не всегда получалось, что прирост коэффициента преломления прямо пропорционален мощности, как мы с легкостью предположили. К тому

же положение осложнялось тем, что несколько эффектов могли действовать вместе.

Ничего не сказали мы и о распределении плотности потока мощности (так называемом профиле интенсивности) по сечению луча 1(г). Ему в основном и посвящена вторая статья о самофокусировке: в 1964 году В. И. Таланов рассчитал профиль интенсивности радиолуча, способного без рассеяния распространяться в плазме. Впоследствии было доказано, что именно за счет выбора особого распределения мощности по сечению луча решается задача самофокусировки в «расфокусирующих» средах — воде, воздухе и других.

Но и это еще не все препятствия на пути открытия. Эксперимент Пилипецкого и Рустамова 1965 года, хотя и подтвердил теоретические выводы, но стал не завершением, а скорее началом нового этапа исследований. Дело в том, что наблюдаемые светящиеся нити ученые истолковали неверно: не как траектории движущихся фокусов, а как постоянные, стабильные волноводные каналы, которые создал себе лазерный пучок и по которым он распространяется без рассеяния.

Лет семь, по крайней мере, о существовании фокусов вообще не подозревали (а мы и об этом сказали как о самоочевидном явлении). Но когда В. И. Таланов рассчитал

Рис. 4. Как ведет себя луч в среде, коэффициент преломления которой уменьшается под действием лазерного луча (таковы, в частности, воз дух и вода)/ Произойдет его саморасфокусировка. Добиться самофокусировки можно, сформировав особый профиль интенсивности — «трубчатый луч». В этом случае внутри «трубки» луч самофокусируется, а вне ее — рассеивается, напоминая по структуре банан, очищаемый от кожуры (это так называемая «банановая самофокусировка»).

условия схлопывания луча в фокус, А. М. Прохоров и В. Н. Луговой — его движение, а В. В. Коробкин обнаружил фокусы лазерных пучков в эксперименте, попутно открылось совсем уже неожиданное. При так называемом гауссовом профиле интенсивности пучка (это наиболее естественное распределение мощности по сечению, когда она максимальна лишь в самом центре и плавно спадает к краям) формируется несколько фокусов! Оказалось, что в этом случае при увеличении мощности каждое новое ее приращение на величину Р., формирует свой, отдельный фокус, отстоящий от излучающей поверхности, так как лучи приходят от все более дальней периферии пучка.

Отсюда ясно, что число фокусов К=Р/Р*, (рис. За). Но, как правило, фокус нужен один, чтобы собрать в нем всю мощность. Стали искать распределение, при котором повышение мощности луча не ведет к «отчленению» порций критической мощности в отдельные фокусы. Таким оказалось платооб-разное распределение, то есть практически постоянное по всему сечению луча, очень резко спадающее до нуля на краях.

Тут настало время дать ответ к задаче о самофокусировке в воде и воздухе. Как уже говорилось, решается она подбором нужного распределения мощности по сечению пучка. Свойства этих самых распространенных сред таковы, что луч лазера никак не может увеличить их коэффициент преломления, наоборот, лишь уменьшает. Поскольку бороться с явлением невозможно, остается одно: обратить его себе на пользу. Вместо того чтобы пытаться увеличить преломление вблизи оси луча, надо просто уменьшить его на периферии. Если нельзя насыпать холм, можно ровное место окопать канавой. Другими словами, надо сделать луч «трубчатым», для чего достаточно поставить на его оси

Рис. 5. Поведение луча в среде, обладающей резонансными свойствами. Если ее резонансная частота совпадает с частотой лазера, луч не просто сходится в фокус, но и после схлопывания продолжает распространяться по тончайшему волноводу, сечение которого соизмеримо с длиной волны.

18