Техника - молодёжи 1937-11-12, страница 74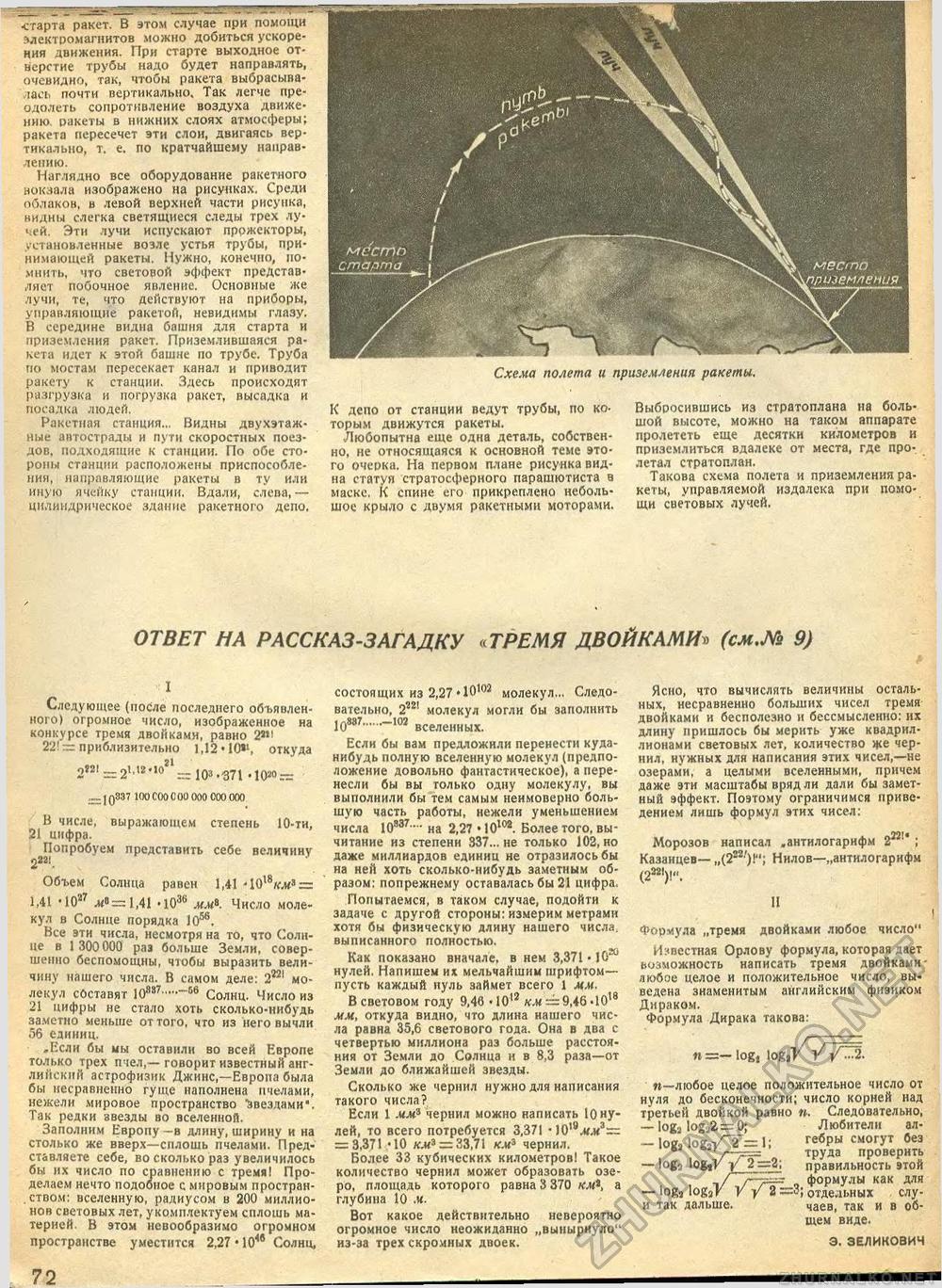

старта ракет. В этом случае при помощи электромагнитов можно добиться ускорения движения. При старте выходное отверстие трубы надо будет направлять, очевидно, так, чтобы ракета выбрасывалась почти вертикально. Так легче преодолеть сопротивление воздуха движению. ракеты в нижних слоях атмосферы; ракета пересечет эти слои, двигаясь вертикально, т. е. по кратчайшему направлению.

Наглядно все оборудование ракетного вокзала изображено на рисунках. Среди облаков, в левой верхней части рисунка, видны слегка светящиеся следы трех лучей. Эти лучи испускают прожекторы, установленные возле устья трубы, принимающей ракеты. Нужно, конечно, помнить, что световой эффект представляет побочное явление. Основные же лучи, те, что действуют на приборы, управляющие ракетой, невидимы глазу. В середине видна башня для старта и приземления ракет. Приземлившаяся ракета идет к этой башне по трубе. Труба по мостам пересекает канал и приводит ракету к станции. Здесь происходят разгрузка и погрузка ракет, высадка и посадка людей.

Ракетная станция... Видны двухэтажные автострады и пути скоростных поездов, подходящие к станции. По обе стороны станции расположены приспособления, направляющие ракеты в ту или иную ячейку станции. Вдали, слева,— цилиндрическое здание ракетного депо.

К депо от станции ведут трубы, по которым движутся ракеты.

Любопытна еще одна деталь, собственно, не относящаяся к основной теме этого очерка. На первом плане рисунка видна статуя стратосферного парашютиста в маске. К спине его прикреплено небольшое крыло с двумя ракетными моторами.

Выбросившись из стратоплана на большой высоте, можно на таком аппарате пролететь еще десятки километров и приземлиться вдалеке от места, где пролетал стратоплан.

Такова схема полета и приземления ракеты, управляемой издалека при помощи световых лучей.

Схема полета и приземления ракеты.

ОТВЕТ И А РАССКАЗ-ЗАГАДКУ «ТРЕМЯ ДВОЙКАМИ'» (см.М 9)

I

Следующее (после последнего объявленного) огромное число, изображенное на конкурсе тремя двойками, равно 2^й1

22!—приблизительно 1,12 • 10«¹, откуда

2**i_2^l.tt'W — 1ОЗ.371 • 1020 —

.—-]q837 100 COO 0 00 000 COO 000

В числе, выражающем степень 10-ти, 21 цифра.

Попробуем представить себе величину 2^аа|.

Объем Солнца равен 1,41 " 10¹⁸к.к⁸ == 1,41 "10^а7 -«о = 1,41 -Ю³⁶ мм». Число молекул в Солнце порядка 10⁵⁶.

Все эти числа, несмотря на то, что Солнце в 1 300000 раз больше Земли, совершенно беспомощны, чтобы выразить величину нашего числа. В самом деле: 2^И1 молекул составят 10⁸⁸⁷.....~⁶⁶ Солнц. Число из

21 цифры не стало хоть сколько-нибудь заметно меньше оттого, что из него вычли 56 единиц.

.Если бы мы оставили во всей Европе только трех пчел,— говорит известный английский астрофизик Джине,—Европа была бы несравненно гуще наполнена пчелами, нежели мировое пространство "Звездами". Так редки звезды во вселенной.

Заполним Европу —в длину, ширину и на столько же вверх—сплошь пчелами. Представляете себе, во сколько раз увеличилось бы их число по сравнению с тремя! Проделаем нечто подобное с мировым прострян-. ством: вселенную, радиусом в 200 миллионов световых лет, укомплектуем сплошь материей. В этом невообразимо огромном пространстве уместится 2,27 • 10^4в Солнц,

состоящих из 2,27-Ю¹⁰² молекул.,. Следовательно, 2^т молекул могли бы заполнить Ю⁸⁸⁷......~¹⁰² вселенных.

Если бы вам предложили перенести куда-нибудь полную вселенную молекул (предположение довольно фантастическое), а перенесли бы вы только одну молекулу, вы выполнили бы тем самым неимоверно большую часть работы, нежели уменьшением числа Ю^вз7— на 2,27 • Ю¹⁰². Более того, вычитание из степени 337... не только 102, но даже миллиардов единиц не отразилось бы на ней хоть сколько-нибудь заметным образом: попрежнему оставалась бы 21 цифра.

Попытаемся, в таком случае, подойти к задаче с другой стороны: измерим метрами хотя бы физическую длину нашего числа, выписанного полностью.

Как показано вначале, в нем 3,371 • 10^го нулей. Напишем их мельчайшим шрифтом— пусть каждый пуль займет всего 1 мм.

В световом году 9,46 • 10¹² км = 9,46-10¹⁸ мм, откуда видно, что длина нашего числа равна 35,6 светового года. Она в два с четвертью миллиона раз больше расстояния от Земли до Солнца и в 8,3 раза—от Земли до ближайшей звезды.

Сколько же чернил нужно для написания такого числа?

Если 1 мм³ чернил можно написать № нулей, то всего потребуется 3,371 • 10^,9лж³=г = 3,371.-10 км* = 33,71 км³ чернил.

Более 33 кубических километров! Такое количество чернил может образовать озеро, площадь которого равна 3 370 км*, а глубина 10 м.

Вот какое действительно невероятно огромное число неожиданно „вынырнуло" из-за трех скромных двоек.

Ясно, что вычислять величины остальных, несравненно больших чисел тремя двойками и бесполезно и бессмысленно: их длину пришлось бы мерить уже квадрил-лионами световых лет, количество же чернил, нужных для написания этих чисел,—не озерами, а целыми вселенными, причем даже эти масштабы вряд ли дали бы заметный эффект. Поэтому ограничимся приведением лишь формул этих чисел:

Морозов написал .антилогарифм 2²²¹" Казанцев— ,,(2²²')!"; Нилов—„антилогарифм (2⁴²¹)!".

И

Формула „тремя двойками любое число" Известная Орлову формула, которая дает возможность написать тремя двойками-любое целое и положительное число, выведена знаменитым английским физиком Дираком.

Формула Дирака такова:

«=- log, log,У У /...2.

м—любое целое положительное число от нуля до бесконечности; число корней над третьей двойкой равно «. Следовательно,

— log₂ log₃2 = 0; Любители ал-

— 1ог, log,yT:=l; гебры смогут без

⁶ ">-г= труда проверить

— logj log,У у 2=2; правильность этой

/ /-4= . формулы как для

— logs Iog₃ V у у 2 =3; отдельных еду-и так дальше. чаев, так и в общем виде.

Э. ЗЕЛИКОВИЧ