Техника - молодёжи 1971-03, страница 68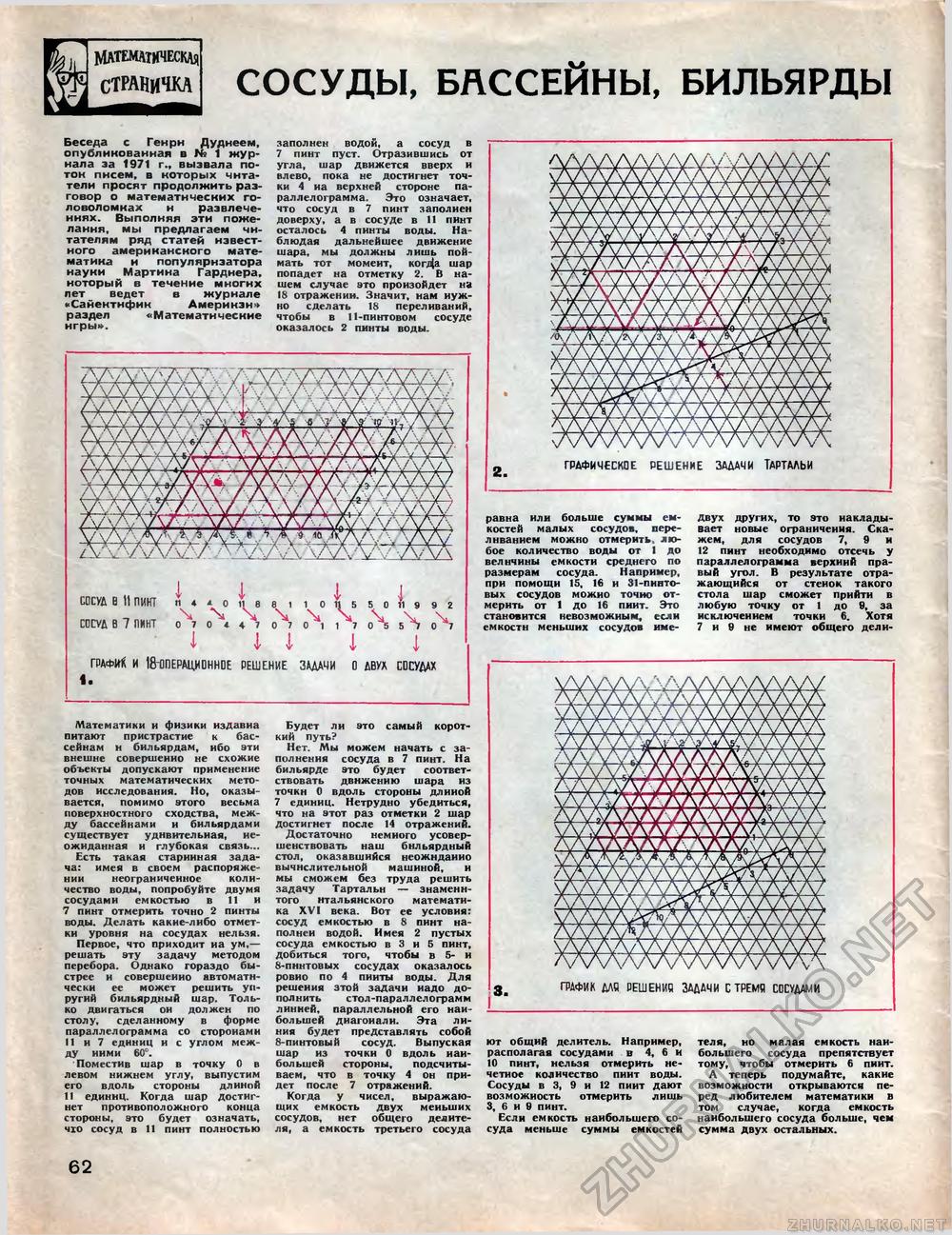

Математическая СТРАНИЧКА

сосуды, бассейны, бильярды

Беседа с Геирн Дуднеем, опубликованная в N9 1 журнала за 1971 г., вызвала по-тон писем, в которых читатели просят продолжить разговор о математических головоломках н развлечениях. Выполняя эти пожелания, мы предлагаем читателям ряд статей известного американского математика и популяризатора науки Мартина Гарднера, ноторый в течение многих лет ведет в журнале «Сайентнфик Америнэнч раздел «Математические игры».

заполнен водой, а сосуд в 7 пинт пуст. Отразившись от угла, шар движется вверх и влево, пока не достигнет точки 4 иа верхней стороне параллелограмма Это означает, чю сосуд в 7 пинт заполнен доверху, а в сосуде в 11 пинт осталось 4 пинты воды. Наблюдая дальнейшее движение шара, мы должны лишь поймать тот момент, когДа шар попадет на отметку 2. В нашем случае это произойдет на 18 отражении. Значит, нам нужно сделать 18 переливаний, чтобы в 11-пинтовом сосуде оказалось 2 пинты воды.

СОСУД в (1

сосуд в 7

ГРАФИ* 1.

11 11 Л «*0 11 6811 0 1} 550 11 992

070*4707011 70 5 570 7

l 1 i i j

и 181ШЕРАЦИ0НН0Е РЕШЕНИЕ ЗАДАЧИ О ДВУХ СОСУДАХ

пикт

пинт

Математики и физики издавна питают пристрастие к бассейнам н бильярдам, ибо эти внешне совершенно не схожие объекты допускают применение точных математических методов исследования. Но, оказывается, помимо этого весьма поверхностного сходства, между бассейнами и бильярдами существует удивительная, неожиданная и глубокая связь...

Есть такая старинная задача: имея в своем распоряжении неограниченное количество воды, попробуйте двумя сосудами емкостью в 11 и 7 пинт отмерить точно 2 пинты воды. Делать какие-либо отметки уровня на сосудах нельзя.

Первое, что приходит иа ум,— решать эту задачу методом перебора. Однако гораздо быстрее и совершенно автоматически ее может решить упругий бильярдный шар. Только двигаться ои должен по столу, сделанному в форме параллелограмма со сторонами 11 и 7 единиц и с углом между ними 60°.

Поместив шар в точку 0 в левом нижнем углу, выпустим его вдоль стороны длиной 11 единиц. Когда шар достигнет противоположного конца стороны, это будет означать, чго сосуд в 11 пинт полностью

равна или больше суммы емкостей малых сосудов, переливанием можно отмерить, любое количество воды от 1 до величины емкости среднего по размерам сосуда. Например, при помощи 15, 16 и 31-пннто-вых сосудов можно точно отмерить от 1 до 16 пиит. Это становится невозможным, если емкости меньших сосудов име-

двух других, то это накладывает новые ограничения. Скажем, для сосудов 7, 9 н 12 пинт необходимо отсечь у параллелограмма верхний правый угол. В результате отражающийся от стеиок такого стола шар сможет прийти в любую точку от 1 до 9, за исключением точки 6. Хотя 7 и 9 не имеют общего дели-

Будет ли это самый короткий путь?

Нет. Мы можем начать с заполнения сосуда в 7 пинт. На бильярде это будет соответствовать движению шара из точки 0 вдоль стороны длиной 7 единиц. Нетрудно убедиться, что на этот раз отметки 2 шар достигнет после 14 отражений.

Достаточно немного усовершенствовать наш бильярдный стол, оказавшийся неожиданно вычислительной машиной, и мы сможем без труда решить задачу Тартальн — знаменитого итальянского математика XVI века. Вот ее условия: сосуд емкостью в 8 пинт наполнен водой. Имея 2 пустых сосуда емкостью в 3 и 5 пинт, добиться того, чтобы в 5- и 8-пннтовых сосудах оказалось ровно по 4 пииты воды. Для решения этой задачи надо дополнить стол-параллелограмм линией, параллельной его наибольшей диагонали. Эта линия будет представлять собой 8-пинтовыЙ сосуд. Выпуская шар из точки 0 вдоль наибольшей стороны, подсчитываем, что в точку 4 он придет после 7 отражений.

Когда у чисел, выражающих емкость двух меньших сосудов, нет общего делителя, а емкость третьего сосуда

з.

график mb решения зддлчи стремя сосудами

ют общий делитель. Например, располагая сосудами в 4, 6 и 10 пинт, нельзя отмерить нечетное количество пиит воды. Сосуды в 3, 9 и 12 пиит дают возможность отмерить лишь 3, 6 и 9 пинт.

Если емкость наибольшего сосуда меньше суммы емкостей

теля, но малая емкость наибольшего сосуда препятствует тому, чтобы отмерить 6 пиит.

А теперь подумайте, какие возможности открываются перед любителем математики в том случае, когда емкость наибольшего сосуда больше, чем сумма двух остальных.

62