Техника - молодёжи 1976-04, страница 46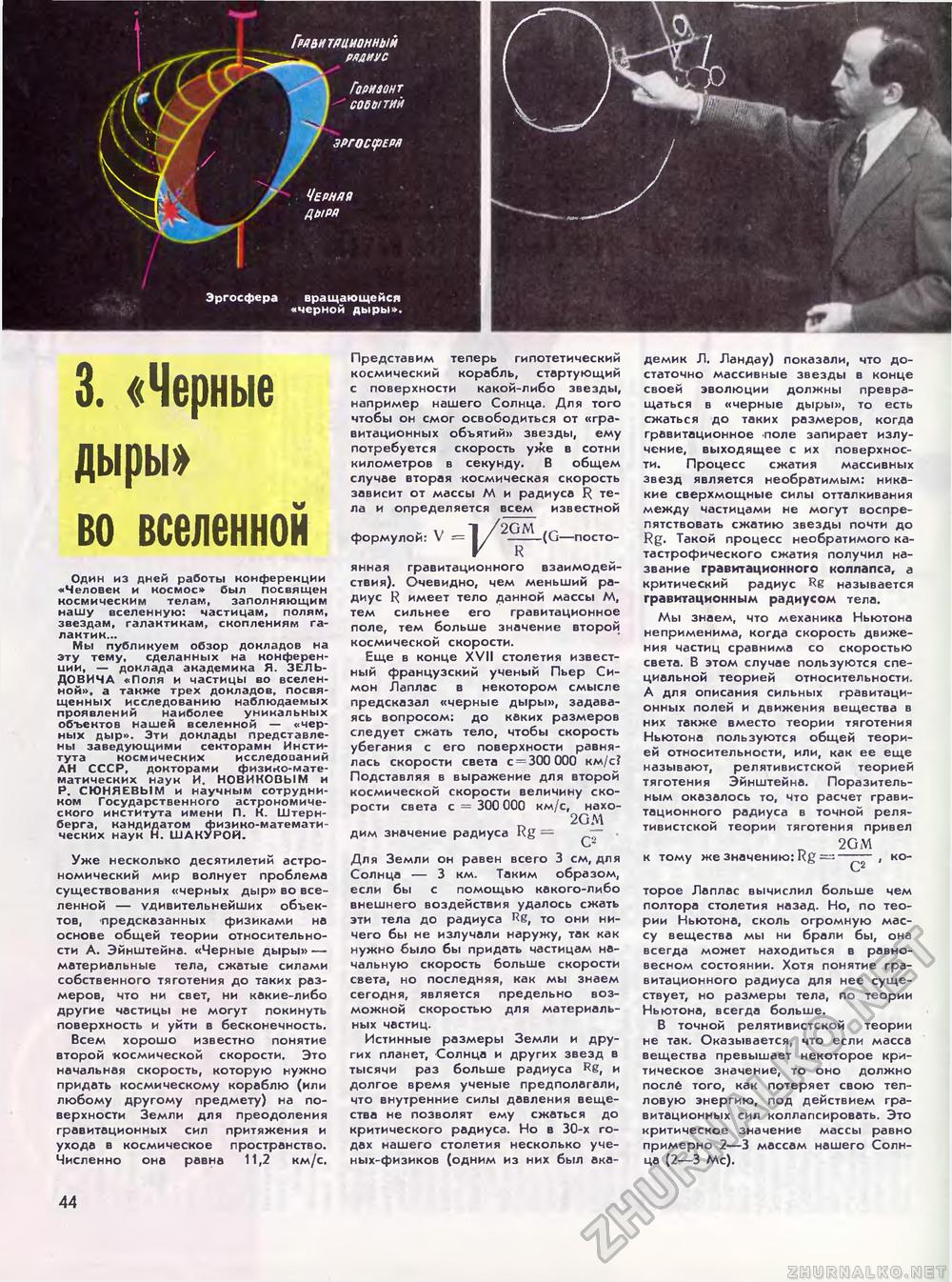

Эргосфера вращающейся «черной дыры».

3. «Черные дыры» во вселенной

Один из дней работы конференции «Человек и космос» был посвящен космическим телам, заполняющим нашу вселенную: частицам, полям, звездам, галактикам, скоплениям галактик...

Мы публикуем обзор докладов на эту тему, сделанных на конференции, — доклада академика Я. ЗЕЛЬДОВИЧА «Поля и частицы во вселенной», а также трех докладов, посвященных исследованию наблюдаемых проявлений наиболее уникальных объектов нашей вселенной — «черных дыр». Эти доклады представлены заведующими секторами Института космических исследований АН СССР, докторами физико-математических наук И. НОВИКОВЫМ и Р. СЮНЯЕВЫМ и научным сотрудником Государственного астрономического института имени П. К. Штернберга, кандидатом физино-математи-ческих наук Н. ШАКУРОИ.

Уже несколько десятилетий астрономический мир волнует проблема существования «черных дыр» во вселенной — удивительнейших объектов, предсказанных физиками на основе общей теории относительности А. Эйнштейна. «Черные дыры» — материальные тела, сжатые силами собственного тяготения до таких размеров, что ни свет, ни какие-либо другие частицы не могут покинуть поверхность и уйти в бесконечность.

Всем хорошо известно понятие второй космической скорости. Это начальная скорость, которую нужно придать космическому кораблю (или любому другому предмету) на поверхности Земли для преодоления гравитационных сил притяжения и ухода в космическое пространство. Численно она равна 11,2 км/с.

Представим теперь гипотетический космический корабль, стартующий с поверхности какой-либо звезды, например нашего Солнца. Для того чтобы он смог освободиться от «гравитационных объятий» звезды, ему потребуется скорость уже в сотни километров в секунду. В общем случае вторая космическая скорость зависит от массы М и радиуса R тела и определяется всем известной

_ _v I /2GM ,_г формулой: V = I/ -((j—посто-

V R

янная гравитационного взаимодействия). Очевидно, чем меньший радиус R имеет тело данной массы М, тем сильнее его гравитационное поле, тем больше значение второй космической скорости.

Еще в конце XVII столетия известный французский ученый Пьер Симон Лаплас в некотором смысле предсказал «черные дыры», задаваясь вопросом: до каких размеров следует сжать тело, чтобы скорость убегания с его поверхности равнялась скорости света с = 300 ООО км/с? Подставляя в выражение для второй космической скорости величину скорости света с = 300 ООО км/с, нахо-

2GM

дим значение радиуса Rg = ~

Для Земли он равен всего 3 см, для Солнца — 3 км. Таким образом, если бы с помощью какого-либо внешнего воздействия удалось сжать эти тела до радиуса Re, то они ничего бы не излучали наружу, так как нужно было бы придать частицам начальную скорость больше скорости света, но последняя, как мы знаем сегодня, является предельно возможной скоростью для материальных частиц.

Истинные размеры Земли и других планет. Солнца и других звезд в тысячи раз больше радиуса Rg, и долгое время ученые предполагали, что внутренние силы давления вещества не позволят ему сжаться до критического радиуса. Но в 30-х годах нашего столетия несколько ученых-физиков (одним из них был ака

демик Л. Ландау) показали, что достаточно массивные звезды в конце своей эволюции должны превращаться в «черные дыры», то есть сжаться до таких размеров, когда гравитационное поле запирает излучение, выходящее с их поверхности. Процесс сжатия массивных звезд является необратимым: никакие сверхмощные силы отталкивания между частицами не могут воспрепятствовать сжатию звезды почти до Rg. Такой процесс необратимого катастрофического сжатия получил название гравитационного коллапса, а критический радиус Rg называется гравитационным радиусом тела.

Мы знаем, что механика Ньютона неприменима, когда скорость движения частиц сравнима со скоростью света. В этом случае пользуются специальной теорией относительности. А для описания сильных гравитационных полей и движения вещества в них также вместо теории тяготения Ньютона пользуются общей теорией относительности, или, как ее еще называют, релятивистской теорией тяготения Эйнштейна. Поразительным оказалось то, что расчет гравитационного радиуса в точной релятивистской теории тяготения привел

2GM

к тому же значению: Rg —, которое Лаплас вычислил больше чем полтора столетия назад. Но, по теории Ньютона, сколь огромную массу вещества мы ни брали бы, она всегда может находиться в равновесном состоянии. Хотя понятие гравитационного радиуса для нее существует, но размеры тела, по теории Ньютона, всегда больше.

В точной релятивистской теории не так. Оказывается, что если масса вещества превышает некоторое критическое значение, то оно должно послб того, как потеряет свою тепловую энергию, под действием гравитационных сил коллапсировать. Это критическое значение массы равно примерно 2—3 массам нашего Солнца (2—3 Мс).

44