Техника - молодёжи 1979-10, страница 26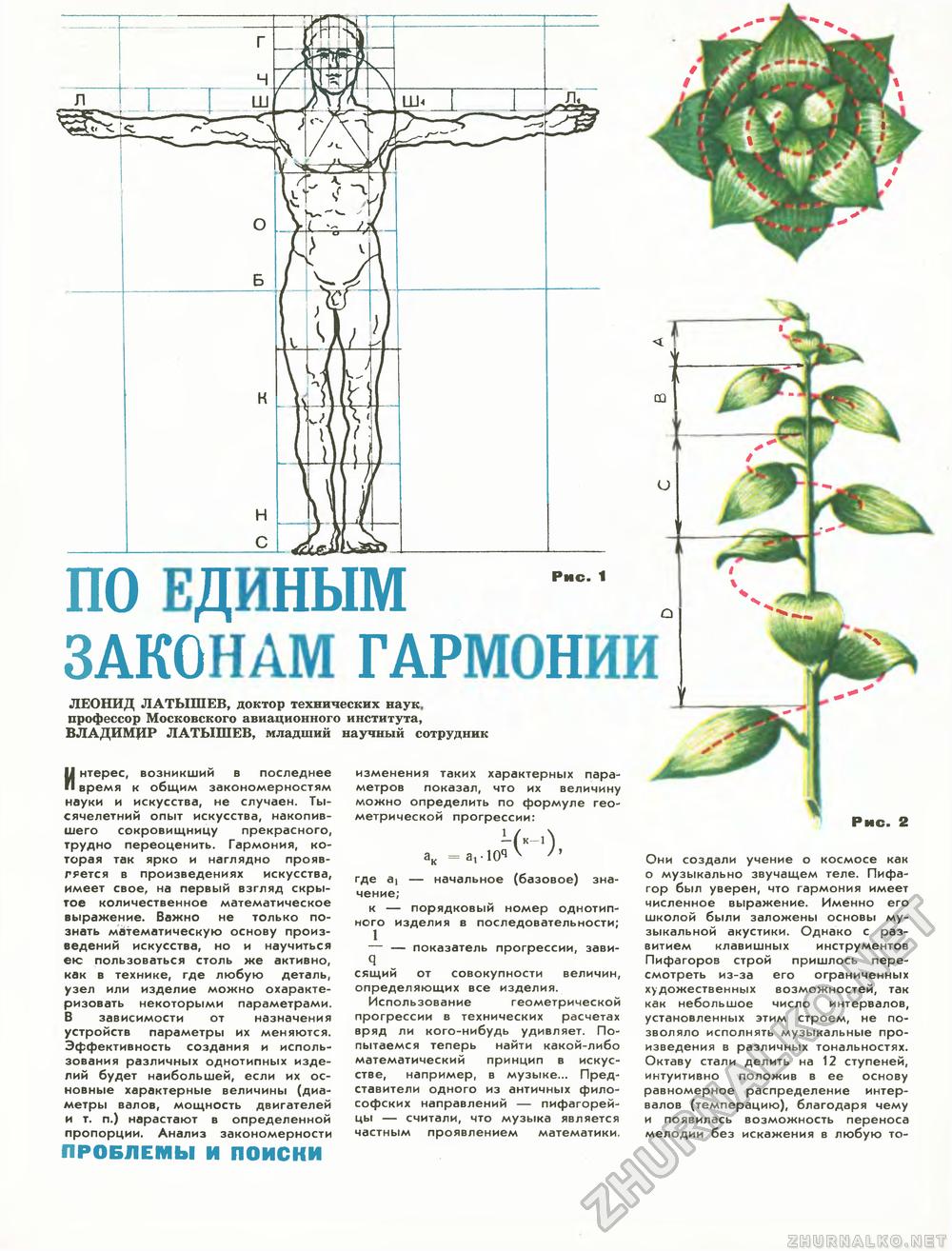

ПО ЕДИНЫМ ' _а ЗАКОНАМ ГАРМОНИИ

ч

ЛЕОНИД ЛАТЫШЕВ, доктор технических наук, профессор Московского авиационного института, ВЛАДИМЦР ЛАТЫШЕВ, младший научный сотрудник

Интерес, возникший в последнее время к общим закономерностям науки и искусства, не случаен. Тысячелетний опыт искусства, накопившего сокровищницу прекрасного, трудно переоценить. Гармония, которая так ярко и наглядно проявляется в произведениях искусства, имеет свое, на первый взгляд скрытое количественное математическое выражение. Важно не только познать математическую основу произведений искусства, но и научиться ею пользоваться столь же активно, как в технике, где любую деталь, узел или изделие можно охарактеризовать некоторыми параметрами. В зависимости от назначения устройств параметры их меняются. Эффективность создания и использования различных однотипных изделий будет наибольшей, если их основные характерные величины (диаметры валов, мощность двигателей и т. п.) нарастают в определенной пропорции. Анализ закономерности

ПРОБЛЕМЫ И ПОИСКИ

изменения таких характерных параметров показал, что их величину можно определить по формуле геометрической прогрессии:

а_к = а_г • 10^ч ^ ^h

где ai — начальное (базовое) значение;

к — порядковый номер однотипного изделия в последовательности;

1

— — показатель прогрессии, зави-

q

сящий от совокупности величин, определяющих все изделия.

Использование геометрической прогрессии в технических расчетах вряд ли кого-нибудь удивляет. Попытаемся теперь найти какой-либо математический принцип в искусстве, например, в музыке... Представители одного из античных философских направлений — пифагорейцы — считали, что музыка является частным проявлением математики.

Рис. 2

Они создали учение о космосе как о музыкально звучащем теле. Пифагор был уверен, что гармония имеет численное выражение. Именно его школой были заложены основы музыкальной акустики. Однако с развитием клавишных инструментов Пифагоров строй пришлось пересмотреть из-за его ограниченных художественных возможностей, так как небольшое число интервалов, установленных этим строем, не позволяло исполнять музыкальные произведения в различных тональностях. Октаву стали делить на 12 ступеней, интуитивно положив в ее основу равномерное распределение интервалов (темперацию), благодаря чему и появилась возможность переноса мелодии без искажения в любую то