Юный техник 1979-04, страница 22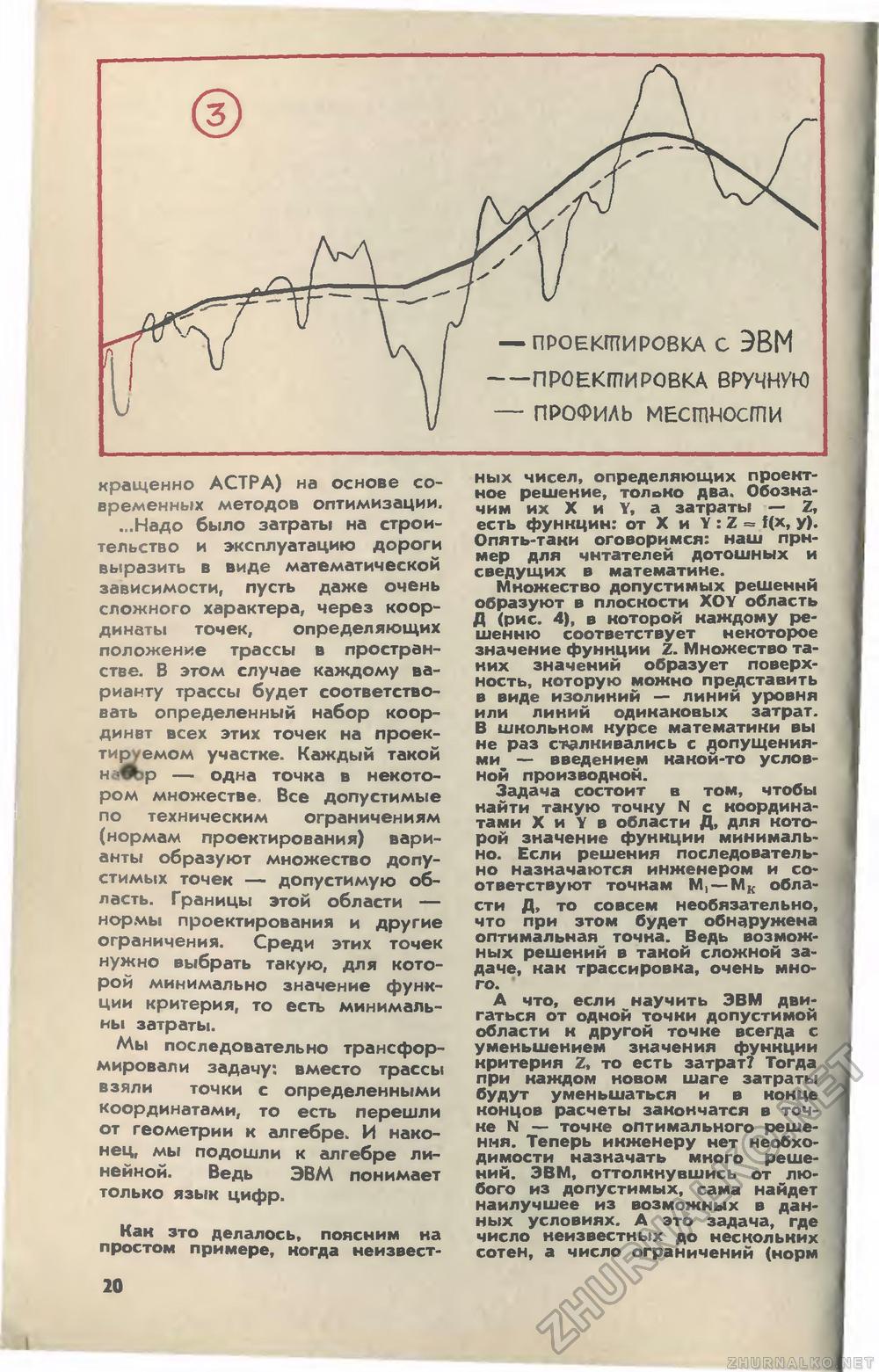
кращенно АСТРА) на основе современных методов оптимизации. ...Надо было затраты на строительство и эксплуатацию дороги выразить в виде математической зависимости, пусть даже очень сложного характера, через координаты точек, определяющих положение трассы в пространстве. В этом случае каждому варианту трассы будет соответствовать определенный набор коор-динвт всех этих точек на проектируемом участке. Каждый такой н<Л>р — одна точка в некотором множестве. Все допустимые по техническим ограничениям (нормам проектирования) варианты образуют множество допустимых точек — допустимую область. Границы этой области — нор<лы проектирования и другие ограничения. Среди этих точек нужно выбрать такую, для которой минимально значение функции критерия, то есть минимальны затраты. Мы последовательно трансформировали задачу: вместо трассы взяли точки с определенными координатами, то есть перешли от геометрии к алгебре. И наконец, мы подошли к алгебре линейной. Ведь ЭВМ понимает только язык цифр. Как это делалось, поясним на простом примере, когда неизвест- 20 ных чисел, определяющих проектное решение, толвко два. Обозначим их X и Y, а затраты — Z, есть функции: от X и Y: Z = f(x, у). Опять-таки оговоримся: наш пример для читателей дотошных и сведущих в математине. Множество допустимых решений образуют в плоскости XOY область Д (рис. 4), в которой каждому решению соответствует некоторое значение фуннции Z. Множество та-них значений образует поверхность, которую можно представить в виде изолиний — линий уровня или линий одинаковых затрат. В школьном курсе математики вы не раз сталкивались с допущениями — введением какой-то условной производной. Задача состоит в том, чтобы найти такую точку N с координатами X и Y в области Д, для которой значение функции минимально. Если решения последовательно назначаются инженером и соответствуют точнам М, — Мк области Д, то совсем необязательно, что при этом будет обнаружена оптимальная точна. Ведь возможных решений в такой сложной задаче, как трассировка, очень много. ' А что, если научить ЭВМ двигаться от одной точки допустимой области к другой точке всегда с уменьшением значения функции критерия Z, то есть затрат? Тогда при каждом новом шаге затраты будут уменьшаться и в конце концов расчеты закончатся в точке N — точке оптимального решения. Теперь инженеру нет необходимости назначать много решений. ЭВМ, оттолкнувшись от любого из допустимых, сама найдет наилучшее из возможных в данных условиях. А это задача, где число неизвестных до нескольких сотен, а число ограничений (норм |








