Юный техник 1985-07, страница 61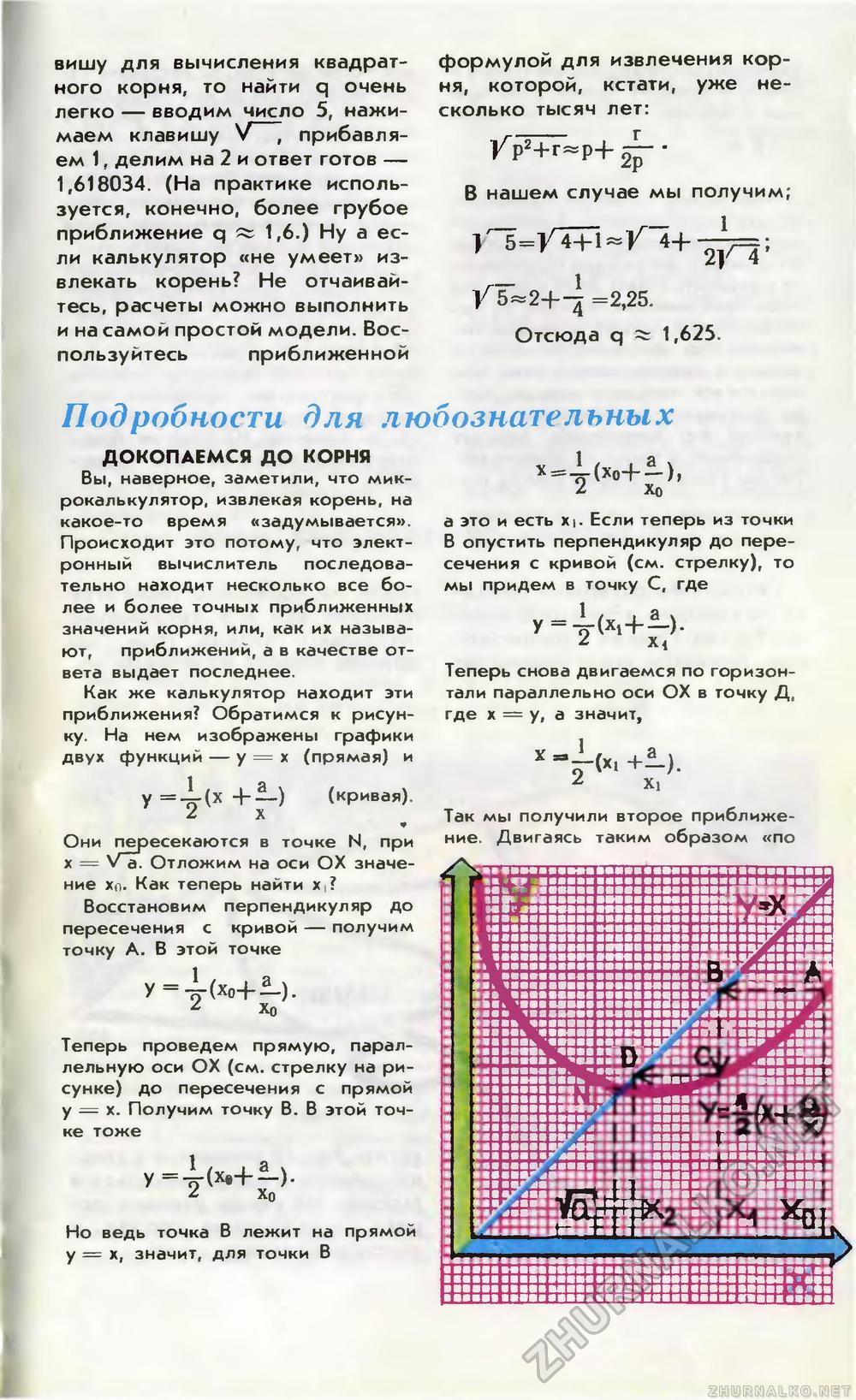

вишу для вычисления квадратного корня, то найти q очень легко — вводим число 5, нажимаем клавишу V \ прибавляем 1, делим на 2 и ответ готов — 1,618034. (На практике используется, конечно, более грубое приближение q » 1,6.) Ну а если калькулятор «не умеет» извлекать корень? Не отчаивайтесь, расчеты можно выполнить и на самой простои модели. Воспользуйтесь приближенной

формулой для извлечения корня, которой, кстати, уже несколько тысяч лет:

В нашем случае мы получим;

4+

— 1

_г— 1

2^4'

V 5«2+-7 =2,25.

Отсюда q ^ 1,625.

Подробности для любознательных

ДОКОПАЕМСЯ ДО КОРНЯ

Вы, наверное, заметили, что микрокалькулятор, извлекая корень, на какое-то время «задумывается». Происходит это потому, что электронный вычислитель последовательно находит несколько все более и более точных приближенных значений корня, или, как их называют, приближений, а в качестве ответа выдает последнее.

Как же калькулятор находит эти приближения? Обратимся к рисунку. На нем изображены графики двух функций — у = х (прямая) и

у-±<*+г->

(кривая).

Они пересекаются в точке N, при х = Va. Отложим на оси ОХ значение хп. Как теперь найти х,?

Восстановим перпендикуляр до пересечения с кривой — получим точку А. В этой точке

у = 1(хо+®-).

¹ Хо

Теперь проведем прямую, параллельную оси ОХ (см. стрелку на рисунке) до пересечения с прямой у = х. Получим точку В. В этой точке тоже

£ х₀

Но ведь точка В лежит на прямой у = х, значит, для точки В

2 х₀

а это и есть Х|. Если теперь из точки В опустить перпендикуляр до пересечения с кривой (см. стрелку), то мы придем в точку С, где

у = * (XJ+®.).

г х₄

Теперь снова двигаемся по горизонтали параллельно оси ОХ в точку Д, где х = у, а значит,

^г XI

Так мы получили второе приближение. Двигаясь таким образом «по