Юный техник 1989-01, страница 36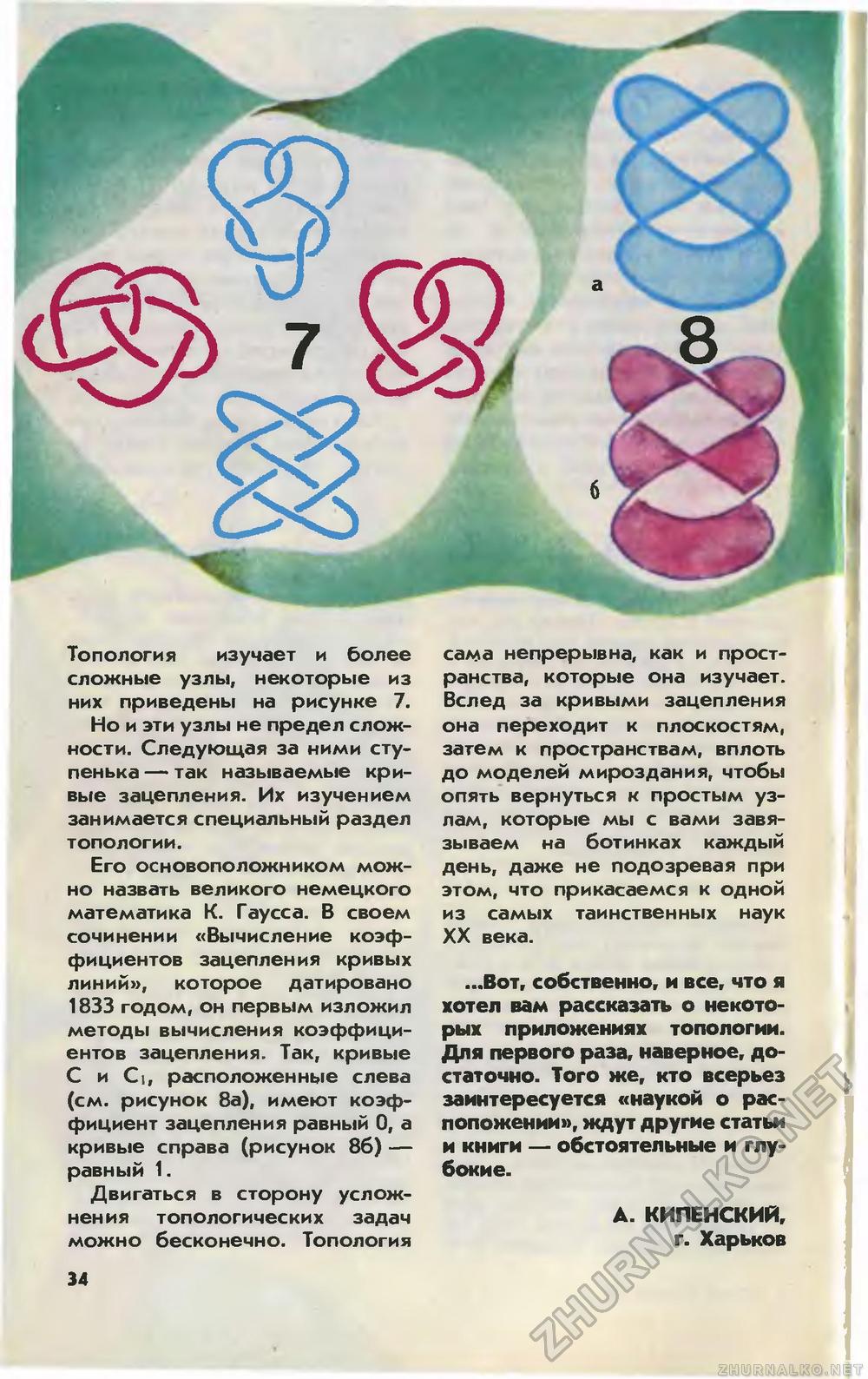

Топология изучает и более сложные узлы, некоторые из них приведены на рисунке 7.

Но и эти узлы не предел сложности. Следующая за ними ступенька — так называемые кривые зацепления. Их изучением занимается специальный раздел топологии.

Его основоположником можно назвать великого немецкого математика К. Гаусса. В своем сочинении «Вычисление коэффициентов зацепления кривых линий», которое датировано 1833 годом, он первым изложил методы вычисления коэффициентов зацепления. Так, кривые С и Ci, расположенные слева (см. рисунок 8а), имеют коэффициент зацепления равный 0, а кривые справа (рисунок 86) — равный 1.

Двигаться в сторону усложнения топологических задач можно бесконечно. Топология

сама непрерывна, как и пространства, которые она изучает. Вслед за кривыми зацепления она переходит к плоскостям, затем к пространствам, вплоть до моделей мироздания, чтобы опять вернуться к простым узлам, которые мы с вами завязываем на ботинках каждый день, даже не подозревая при этом, что прикасаемся к одной из самых таинственных наук XX века.

...Вот, собственно, и все, что я хотел вам рассказать о некоторых приложениях топологии. Для первого раза, наверное, достаточно. Того же, кто всерьез заинтересуется «наукой о расположении», ждут другие статьи и книги — обстоятельные и глубокие.

А. КИПЕНСКИЙ, г. Харьков

34