Техника - молодёжи 1974-06, страница 8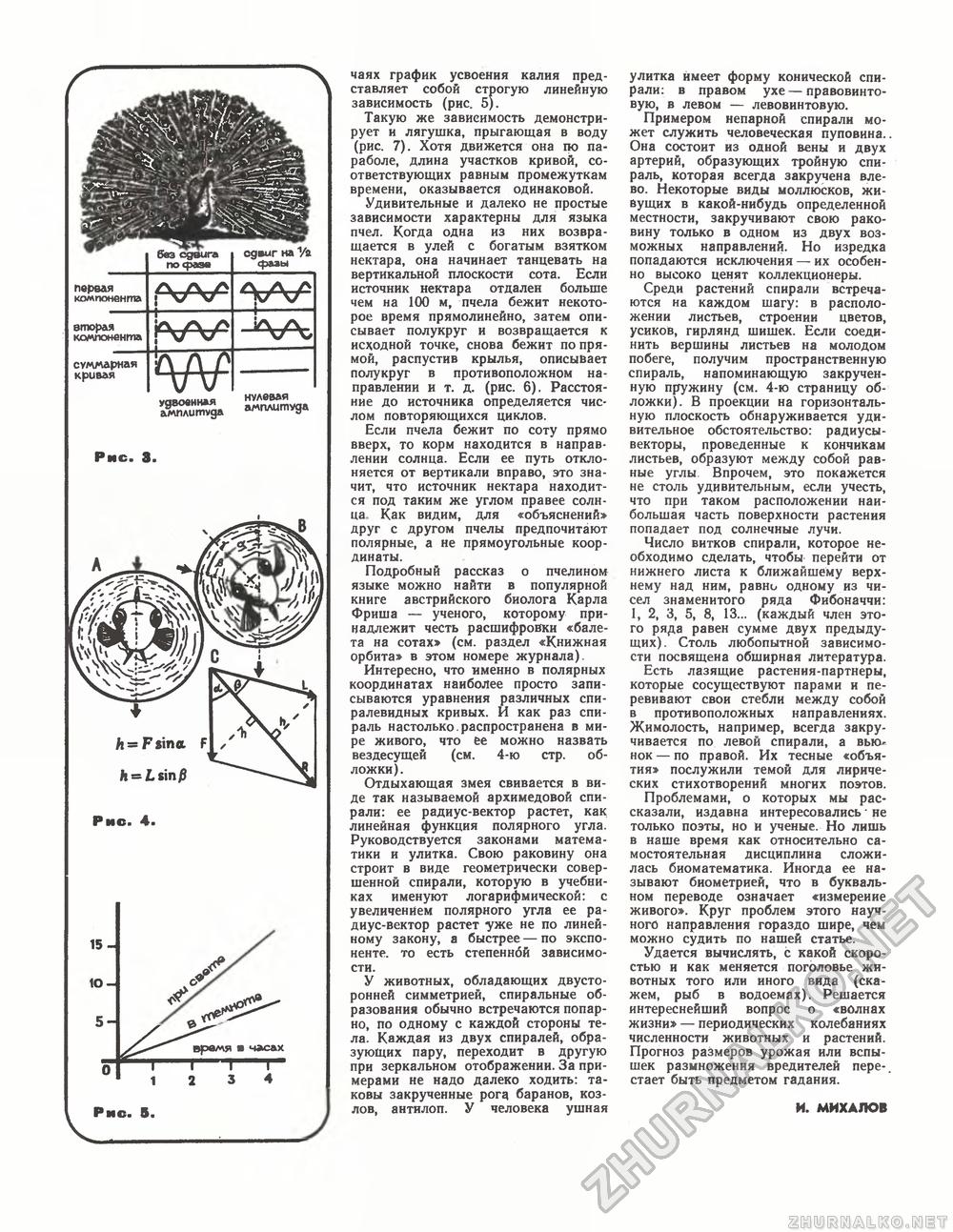

первая компонента

вторая компонента

су/лмарная кривая

без сдвига пофавв

ЛУЧ/⁴

iw⁵

W

сдвиг на Уа фазы

ЛУЧ/⁴

ЯГда амплитуда

Рис. 3.

Рис. 4.

Рис. В.

чаях график усвоения калия представляет собой строгую линейную зависимость (рис. 5).

Такую же зависимость демонстрирует и лягушка, прыгающая в воду (рис. 7). Хотя движется она по параболе, длина участков кривой, соответствующих равным промежуткам времени, оказывается одинаковой.

Удивительные и далеко не простые зависимости характерны для языка пчел. Когда одна из них возвращается в улей с богатым взятком нектара, она начинает танцевать на вертикальной плоскости сота. Если источник нектара отдален больше чем на 100 м, пчела бежит некоторое время прямолинейно, затем описывает полукруг и возвращается к исходной точке, снова бежит по прямой, распустив крылья, описывает полукруг в противоположном направлении и т. д. (рис. 6). Расстояние до источника определяется числом повторяющихся циклов.

Если пчела бежит по соту прямо вверх, то корм находится в направлении солнца. Если ее путь отклоняется от вертикали вправо, это значит, что источник нектара находится под таким же углом правее солнца. Как видим, для «объяснений» друг с другом пчелы предпочитают полярные, а не прямоугольные координаты.

Подробный рассказ о пчелином языке можно найти в популярной книге австрийского биолога Карла Фриша — ученого, которому принадлежит честь расшифровки «балета на сотах» (см. раздел «Книжная орбита» в этом номере журнала).

Интересно, что именно в полярных координатах наиболее просто записываются уравнения различных спиралевидных кривых. И как раз спираль настолько.распространена в мире живого, что ее можно назвать вездесущей (см. 4-ю стр. обложки).

Отдыхающая змея свивается в виде так называемой архимедовой спирали: ее радиус-вектор растет, как линейная функция полярного угла. Руководствуется законами математики и улитка. Свою раковину она строит в виде геометрически совершенной спирали, которую в учебниках именуют логарифмической: с увеличением полярного угла ее ра-диус-вектор растет уже не по линейному закону, а быстрее — по экспоненте. то есть степенной зависимости.

У животных, обладающих двусторонней симметрией, спиральные образования обычно встречаются попарно, по одному с каждой стороны тела. Каждая из двух спиралей, образующих пару, переходит в другую при зеркальном отображении. За примерами не надо далеко ходить: таковы закрученные рога баранов, козлов, антилоп. У человека ушная

улитка имеет форму конической спирали: в правом ухе — правовинто-вую, в левом — левовинтовую.

Примером непарной спирали может служить человеческая пуповина.. Она состоит из одной вены и двух артерий, образующих тройную спираль, которая всегда закручена влево. Некоторые виды моллюсков, живущих в какой-нибудь определенной местности, закручивают свою раковину только в одном из двух возможных направлений. Но изредка попадаются исключения — их особенно высоко ценят коллекционеры.

Среди растений спирали встречаются на каждом шагу: в расположении листьев, строении цветов, усиков, гирлянд шишек. Если соединить вершины листьев на молодом побеге, получим пространственную спираль, напоминающую закрученную пружину (см. 4-ю страницу обложки). В проекции на горизонтальную плоскость обнаруживается удивительное обстоятельство: радиусы-векторы, проведенные к кончикам листьев, образуют между собой равные углы. Впрочем, это покажется не столь удивительным, если учесть, что при таком расположении наибольшая часть поверхности растения попадает под солнечные лучи.

Число витков спирали, которое необходимо сделать, чтобы перейти от нижнего листа к ближайшему верхнему над ним, равно одному из чисел знаменитого ряда Фибоначчи: 1, 2, 3, 5, 8, 13... (каждый член этого ряда равен сумме двух предыдущих). Столь любопытной зависимости посвящена обширная литература.

Есть лазящие растения-партнеры, которые сосуществуют парами и перевивают свои стебли между собой в противоположных направлениях. Жимолость, например, всегда закручивается по левой спирали, а вьюнок — по правой. Их тесные «объятия» послужили темой для лирических стихотворений многих поэтов.

Проблемами, о которых мы рассказали, издавна интересовались * не только поэты, но и ученые. Но лишь в наше время как относительно самостоятельная дисциплина сложилась биоматематика. Иногда ее называют биометрией, что в буквальном переводе означает «измерение живого». Круг проблем этого научного направления гораздо шире, чем можно судить по нашей статье.

Удается вычислять, с какой скоростью и как меняется поголовье животных того или иного вида (скажем, рыб в водоемах). Решается интереснейший вопрос о «волнах жизни» — периодических колебаниях численности животных и растений. Прогноз размеров урожая или вспышек размножения вредителей пере-, стает быть предметом гадания.

И. МИХАЛОВ